
Clay Bennett
Assignment 8
In this investigation, I will be taking a look at the orthocenter of a triangle. I initially began my investigation by trying to prove that
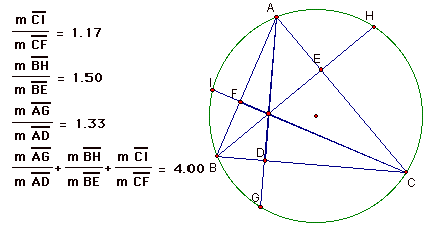
(AG/AD)
+ (BH/BE) + (CI/CF) = 4
I
spent far too much time trying to prove this with no progress. I took it to Dr. Mo Hendon and Dr. Ed
Azoff for guidance and both had no clue what to do. So I gave up the ghost and went for something simpler.
I am
now going to prove that the altitudes of a triangle have a concurrent point,
which is known as the orthocenter.
I
will start with the following arbitrary triangle.
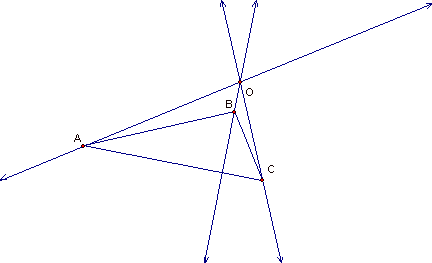
Now
I will proof the altitudes of the triangle are concurrent using linear
algebra. I might as well get some
use out of it since I took the class three times. Note: the * means dot
product.
From my
construction of the altitudes, I know that
(i)
(O-A) *
(B-C) = 0
(ii)
=> (O*B)
– (O*C) – (A*B) + (A*C) = 0
(iii)
(O-B) *
(C-A) = 0
(iv)
=> (O*C)
– (O*A) – (B*C) + (B*A) = 0
(v)
(O-C) *
(B-A) = 0
(vi)
=> (O*B)
– (O*A) – (C*B) + (C*A) = 0
If
I subtract (ii) from (iv) then I get (vi), which proves that the altitudes are
concurrent.