
Sinje Butler
Write-up 4
The CENTROID (G) of a triangle is the common intersection of the three medians.
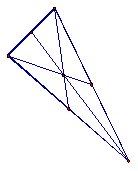
As the shape of the triangle changes the centroid always remains inside. Please see GSP demonstration and move one point of triangle to notice the changes taking place.
The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes.
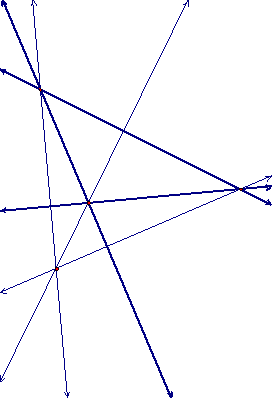
It should be clear that as the shape of the triangle changes, H does not always fall inside the triangle. Please see GSP demonstration and move one point of triangle to notice the changes taking place.
The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. C is on the perpendicular bisector of each side of the triangle. Notice that as the triangle changes shape the circumcenter does not always stay inside. Please see GSP demonstration and move one point of triangle to notice the changes taking place.

Note that the circumcenter is the center of the CIRCUMCIRCLE. The circumcircle is constructed by drawing a segment from the circumcenter to one of the vertices and using this segment as the radius of the circle.
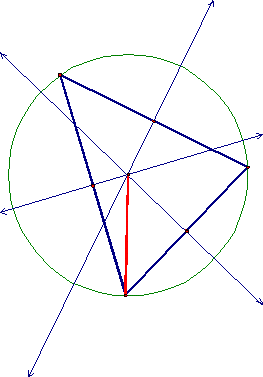
![]()
![]()
![]()
Please see GSP demonstration and move one point of
triangle to notice the changes in the length of the of the radius ![]() .
.
The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. I is on the angle bisector of each angle of the triangle.
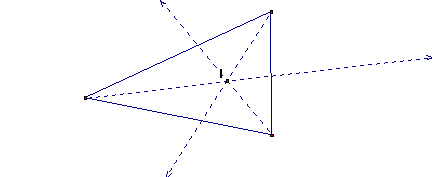
Please see GSP demonstration and move one point of the triangle to notice the changes.
The incenter is the center of the INCIRCLE (the inscribed circle) of the triangle. The incenter is constructed by drawing a segment from the incenter perpendicular to one of the sides of the triangle and using this segment as the radius of the circle.
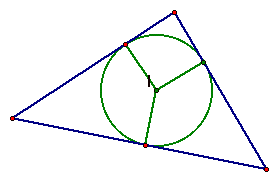
Please see GSP demonstration and move one point of the triangle to notice the changes.
The following is a construction of G, H, C, and I for the same triangle.
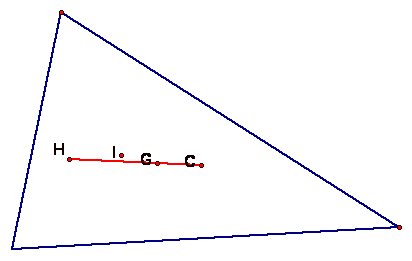
Please see GSP demonstration and move one point of the triangle to notice the changes.