
Sinje
J. Butler
Write-up # 1
The following is the graph of the function
n ![]() .
.

Below is a graph of
n ![]()
n ![]()
n ![]()
and
n ![]() .
.
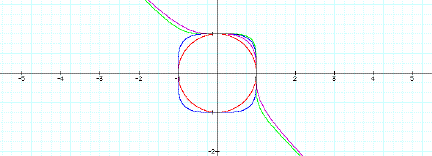
There appears to be several things occurring as the
exponents of
![]()
are raised to higher powers.
1.
The graphs of the equations raised to an odd power
n ![]()
and
n ![]()
are no longer circles. They open up and stretch out. This occurs in an equation that is in
the format of
![]()
for ![]() .
.
The reason is that for any real
number value of x, when x is raised to an odd power, there exists a real number y such that when it is raised to that same power there sum is equal to
one. So it can be predicted that
n
![]()
will look similar to the graphs of
the previous odd powered equations.
This is not the case for the
equation
![]()
because x^2 and y^2 will always be positive numbers,
therefore, x and y are limited
to being values from –1 to 1 where they
cannot both be equal to one at the same time, both be equal to negative one at
the same time, or equal to one
and negative one at the same time.
2.
When
n![]()
is changed to
n ![]()
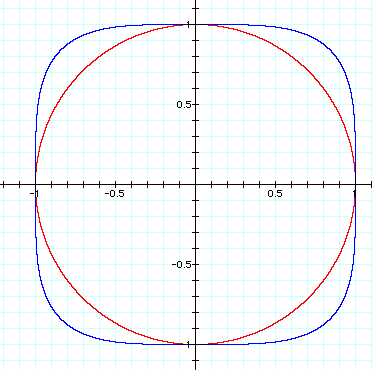
the
curve begins to straighten out in order to take on more of a square shape. Recall,
the concept of distance on the coordinate
plane is based on the Pythagorean Theorem. The theorem states
![]()
where C is the distance from the origin.
We can write
![]()
as
![]()
where 1 is the distance from the origin.
We can easily conclude that for any values of x and y from –1 to1, where x and y are both not equal to 1 , both not equal to –1, or not equal to –1 and 1 at the same time, the distance
from the origin is one. Thus
making the graph a circle.
This is not the case for
![]()
where
![]() > 1.
> 1.
In these equations, the various (x,y) coordinates of a given graph will be different distances form the
origin. The distances from the
origin will increase and decrease through various intervals. This gives the
graph a more square shape.