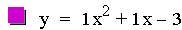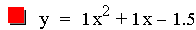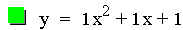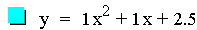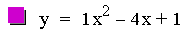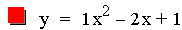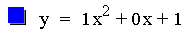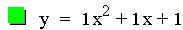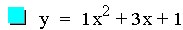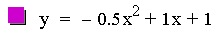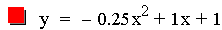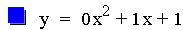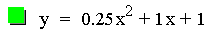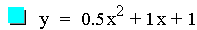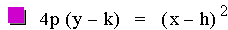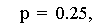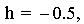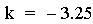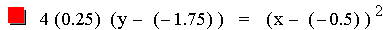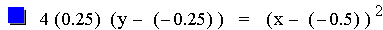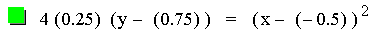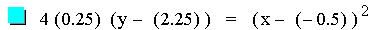Assignment 2: Quadratic Equations
by
Mike Cotton
In this assignment, the quadratic equation ax2
+ bx + c where the constants a, b, & c are varied will be
investigated.
Let's begin the investigation with the equation ax2
+ bx + c where a = 1, b = 1, and c is varied. Let's look at equations
where c equals: -3, -1.5, 0, 1, & 2.5.
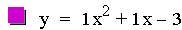
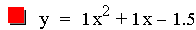

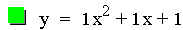
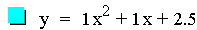
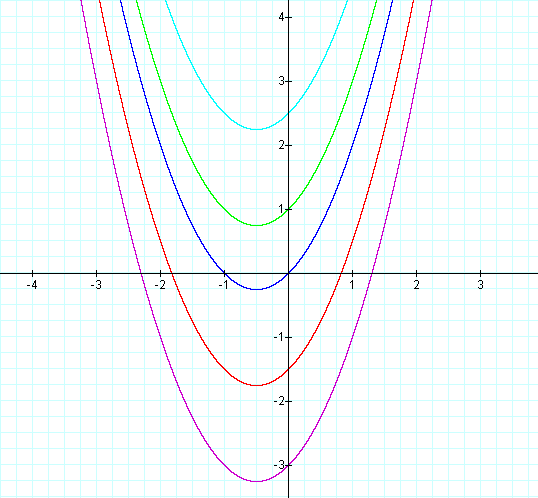
This graph was created by Graphing
Calculator 3.2.
There are several patterns that are noticable. One is that as c becomes
larger the corresponding parabola is further up the y-axis on the
graph. Another item of notice is that the parabola for each equation
intersects the y-axis at its value of c. For example the value for c in
the second equation is
-1.5, and its corresponding parabola crosses the y-axis at -1.5. This
makes sense because x equals zero along the y-axis, so if x = 0 is used
in all the equations above then y would equal c. Also notice that
although all of the parabolas are at different positions on the graph,
they are all the same size.
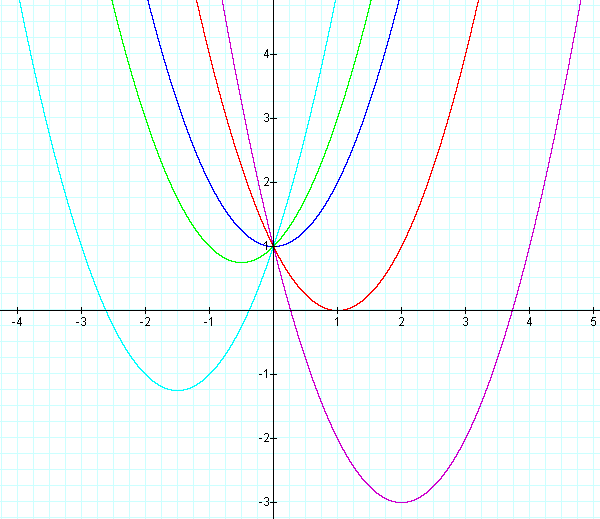
Now let's investigate the same quadratic equation
where this time a = 1, c = 1, and b is varied.
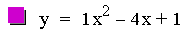
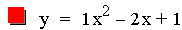
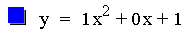
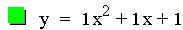
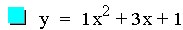
This graph was created by Graphing
Calculator 3.2.
Notice that every one of the parabolas pass through the point (0, 1).
You can probably guess from the previous investigation that this is
because c = 1 for all the equations in this investigation. Also notice
that these parabolas, like the parabolas in the previous investigation,
are all the same size. Another pattern that is noticable is that as b
increases, the vertex of the parabola moves up and to the left until it
passes through the point (0, 1) that was just mentioned. Then the
vertex continues to move left but now downwards. This will be
investigated in more details later in this assignment.
The next investigation of the quadratic equation will
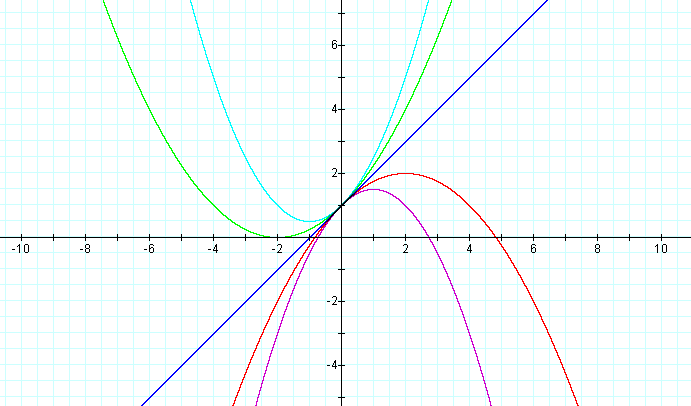
look at the case where b = 1, c = 1, and a is varied.
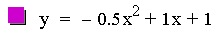
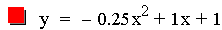
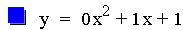
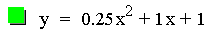
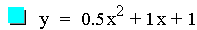
This graph was created by Graphing
Calculator 3.2.
The first item to notice in this investigation is that all of these
parabolas are of different sizes, and there is a line instead of a
parabola for the third
equation. Again notice that all of the parabolas pass through the same
point on the y-axis. It is also worth noticing that when a is positive
the parabola opens upward, and if it is negative it opens downward.
In the investigations above the form of the equation
has been ax2
+ bx + c. There are other forms to represent the same equation. One
form is
y = a(x + (b – (b2 – 4ac)1/2)/2)
(x + (b + (b2
– 4ac)1/2)/2a), where (b ± (b2 –
4ac)1/2)/2a is the quadratic equation. This
form is helpfull when determining the points there the parabola
intersects the x-axis.
Another form is 4p(y – k) =
(x – h)2, which was mentioned in Assignment 1. This form is
useful when investigating the parabola geometically. The variable p
determines the focus of the parabola which effects the shape of the
parabola, and whether the parabola will open up (positive p) or down
(negative p). The variables h and k are the x & y coordinates for
the vertex, (h, k), of the parabola. The vertex is the lowest point of
the parabola if it opens upward, and the highest point if it opens
downward. Let's take a look at some parabolas written in the form 4p(y – k) =
(x – h)2.
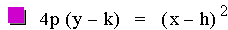
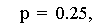
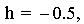
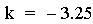
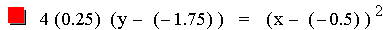
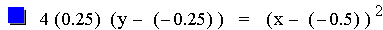
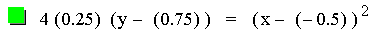
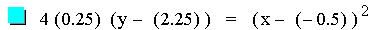
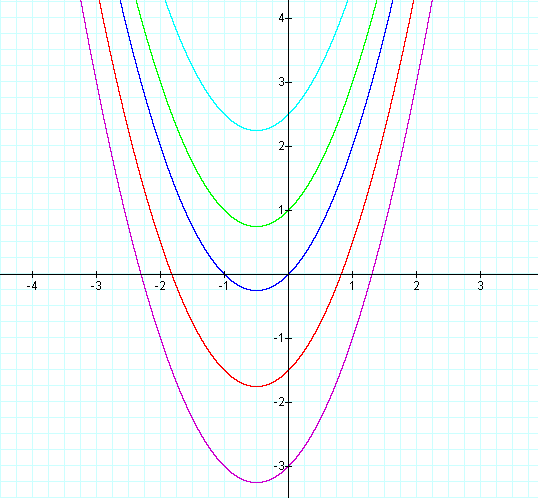
This graph was created by Graphing
Calculator 3.2.
In this investigation the values for p (0.25) and h (-0.5) are
constant, while the value for k varies. Since k is the y-coordinate for
the vertex of the parabola, the parabolas are all the same size
(constant p), all have the same x value (h = -0.5) for the vertex, but
are at different y values. As it turns out, this graph is the same as
the first graph in this assignment. The variables p, h, and k can all
be represented in terms of a, b, and c from the equiation ax2
+ bx + c. p = 1/4a, h = -b/2a, and
k = c – b2/4a.
It can now be understood that if the variable c is changed this only
effects k, which is the y-coordinate of the parabola's vertex. If the
variable b is changed, this effects h & k
which are the x and y coordinates of the vertex. If the variable a is
changed, this effects p, h, & k. With this explained it is
suggested that the previous investigations be reviewed.
Assignment 1
Return to main Page
Assignment 3