

1. Graph
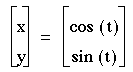
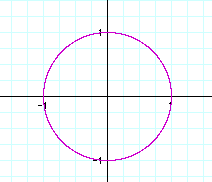
As you can see, the solution appears to be a circle with center at the origin and a radius of 1.
In order to further investigate, I will observe the parametric equations
for various a's and b's.
Let's observe some examples:
1) a=b
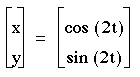
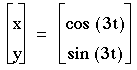
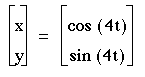
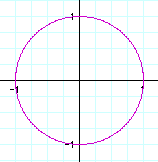
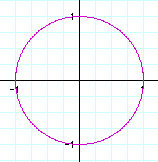
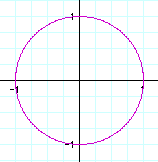
It is obvious that when a=b, then the solution will always be a circle about the origin with a radius of 1.
2)a=2
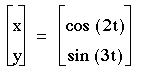
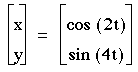
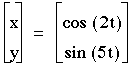
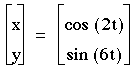
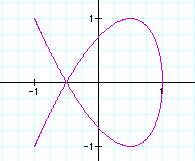
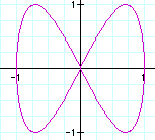
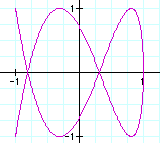
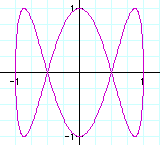
As you can see, when a=2, then the solution is a series of curves that look like loops.
The number of loops depends on b. You can see that the number of loops = 1/2(b).
3) b=2
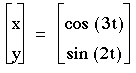
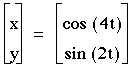
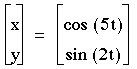
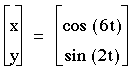
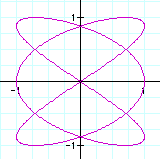
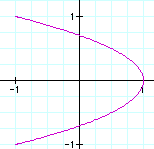
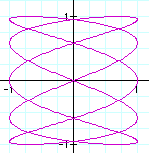
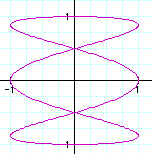
These graphs look very different, so I will look at the ones where a is odd first. When a is odd, you can see that there are always 2 maxs and mins for y, and there are a maxs and mins for x.
When a is even, there appears to only be one max and min for y and 1/2(a) maxs and mins for x. When a=4, this notion is not true. This makes me wonder if this is because a=2b. So, now I will look at some of these examples.
4)a=2b
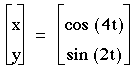
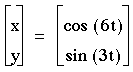
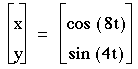
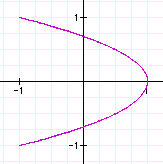
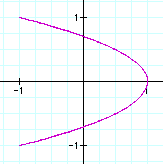
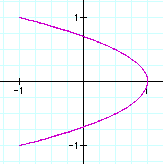
So, it is true that when a=2b the graph is always in this shape.
5) Some other fun examples
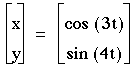
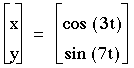
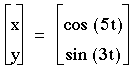

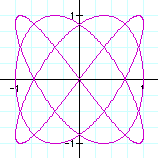
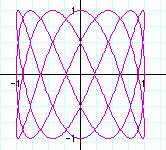
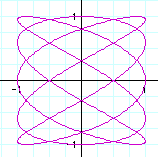
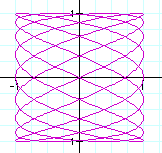
As you can see from these examples, the number of maxs and mins for x is always a, and the number of maxs and mins for y is always b. Another observation is that the graph is always in the boundaries -1<x<1 and -1<y<1.
Another way to help me further my investigation is to look at the parametric equations
for various a's and b's.
Let's observe some examples.
1)a=b
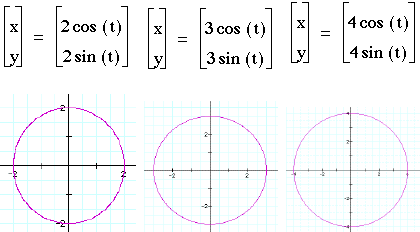
It is obvious that when a=b, the solution is a circle with center at the origin and radius equal to a and b (r=a=b).
2)Some other fun examples
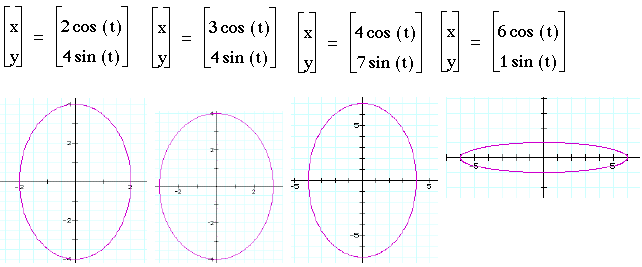
As you can see, the solution is always an ellipse with the center at the origin and the x max=a, x min=-a, y max=b, and y min= -b.