

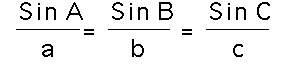 .
.We will prove the Law of Sines for the acute triangle case and the obtuse triangle case.
Let's go!
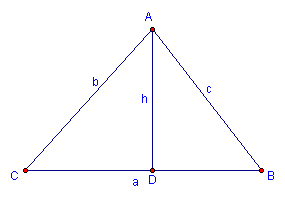
 be an acute triangle with
be an acute triangle with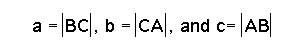 . Notice h
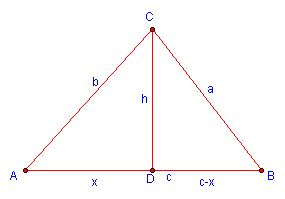
is the perpendicular from A to the line segment BC. It intersects
the segment BC at the point D. Now, two right triangles are formed
and they are
. Notice h
is the perpendicular from A to the line segment BC. It intersects
the segment BC at the point D. Now, two right triangles are formed
and they are If
we want to prove the Law of Sines holds true in this acute case,
it is enough to show that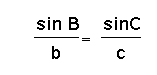 .
.
 .
.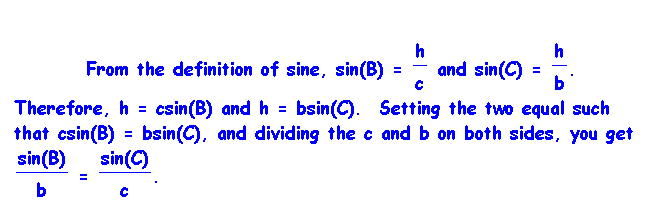
Now we have proved the Law of Sines for the Acute Triangle case!
Let's
continue and try to prove the Law of Sines for the Obtuse Triangle
case....
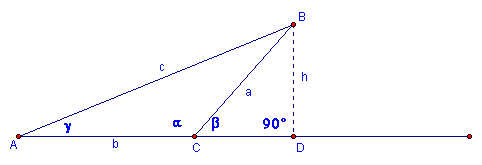
Let
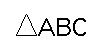 be an obtuse triangle with
be an obtuse triangle with 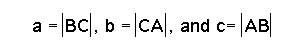 . Notice again
that h is the perpendicular from the point B to the line segment
AC. H intersects the segment AC at the point D.
. Notice again
that h is the perpendicular from the point B to the line segment
AC. H intersects the segment AC at the point D.
Alpha is an obtuse angle and Beta is its supplement. Remember that angles that are supplementary form a line. Therefore, alpha plus Beta form the line with points A,C, and D on it.
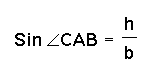 and
and
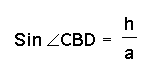 so h = bsin
so h = bsin![]() and h=asin
and h=asin![]() .
.
Setting the two h's equal to one another, we get
bsin![]() =
asin
=
asin![]() .
.
Therefore,
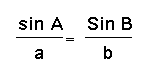 and the Law of Sines works for the Obtuse Triangle
case as well:)
and the Law of Sines works for the Obtuse Triangle
case as well:)
We will prove the Law of Cosines for the acute triangle case and the obtuse triangle case.
Let's go!
Remember
the cosine of an angle is equal to the  .
.
Segment
CD or h is the perpendicular from the point C to the line segment
AB. It intersects the line segment AB at the point D. 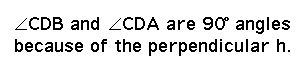
 .
Therefore,
.
Therefore,
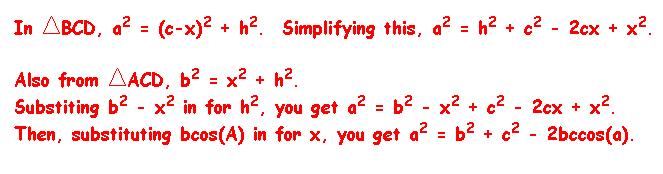 .
.
Therefore,
we have proved the Law of Cosines for the Acute Triangle case.
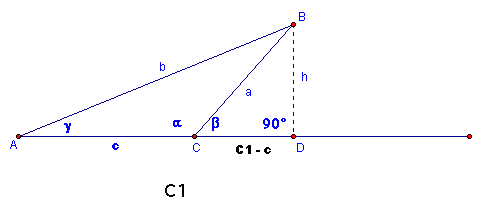
Using the fact that Triangle ADB and Triangle CDB are both right triangles, we can use the Pythagorean Theorem to get...
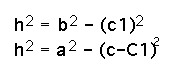
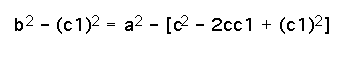
Then
finally, ![]() . So, we have proved the Law of Cosines for the Obtuse
Triangle Case.
. So, we have proved the Law of Cosines for the Obtuse
Triangle Case.