Assignment
11
POLAR
EQUATIONS
In
this investigation, we will look at the equation r = a + bcos(kx).
In
this graph, a and b both equal 1 and k is the integer 1. This
is one version of the n-leaf rose. Let's now compare this to
r
= bcos(kx).
Purple:
Red: 
Notice
that when the a is 0, we have a circle with center (.5,0) and
rdius .5.
It
is interesting to see what will happen when we replace cosine
with sine.
Purple: 
Red: 
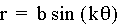
Notice
that the graph has the same characteristics, it just rotates around
the origin.
Now
we will see what happens when a,b,c, and k are varied.
In
this graph, k was increased to a value of 2. Everything else remained
the same. This resulted in the graph splitting into two loops.
For
k = 3:
This
results in three loops.
For
k=4:
This
results in 4 loops.
To
see the pattern from k=1 through 10 click HERE!
What
if a and b remain equal, but they both increase? Click here to check it out.
Next
I will investigate quite a few different equations.
Click HERE to see 
for varying a's.
Click
HERE
to
see 
for varying a's.
**Notice
that this changes the size of the graphs and there is no loop.
Click
HERE to see 
for varying a's.
Click
HERE to see 
for varying a's.
**Notice
that this changes the size of the graph.
Now
I will look at 
.
This
first graph shows when a,b,c, and k are 1.
Now
I will let a and b vary at the same rate.
Click
HERE to see what happens
to the graph.
Now
I will let c vary.
Click
HERE to see the results.
Now
I will let k vary.
Click
HERE to see the results.
The
k seems to be the most interesting change because it changes the
number of lines.
return