Using GSP to explore Tangent Circles

This investigation centers around constructing a circle tangent to two other circles. We can focus on how technology (specifically in this case GSP) aids and encourages exploration.

While this construction is not extremely difficult, it does require several steps. Considering different shapes and configurations of circles could take a great deal of time just to construct separate examples. A student is likely to get bogged down in the steps of the construction and miss the point of the exploration if they are required to start over from scratch for each idea they might have.

Fortunately, programs like GSP make the construction work relatively short and painless so that the user can concentrate on the exploring their construction. For example, there are many cases for constructing a circle tangent to two circles. The two circles may be disjoint. They might intersect each other. One might even be contained in the other circle. These cases are illustrated below (initial circles in red and tangent circle in blue).

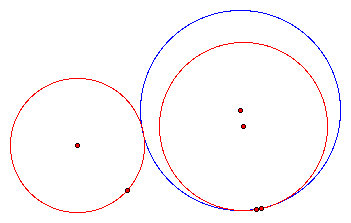
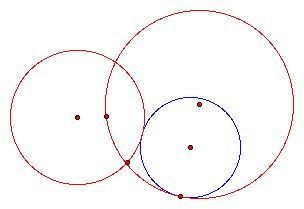
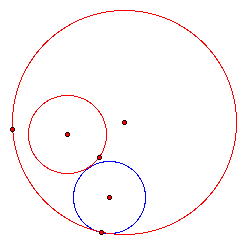
Doing each of these constructions from scratch would be time consuming (and frustrating). GSP, however, allows the user to take the first construction and change the shapes of the two initial circles until they intersect while keeping the tangent circle construction intact. Thus we arrive at the second construction in a matter of seconds. Then to arrive at the third, we just need to move one of the initial circles inside the other.

We can then either save the initial construction or make it into a script tool. Then the user can quickly begin exploring new ideas without having to first take the time to recreate the construction.

Some interesting things to explore in this construction are the loci of the center of the tangent circle. This can quickly and easily be done in GSP by tracing the tangent circle center and animating the arbitrary point on the larger circle used to construct the tangent circle. We show an example of this below (locus in green).

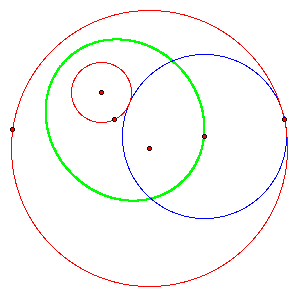
We can then quickly observe that in this case the locus is an ellipse that appears to have foci at the centers of the initial circles. We can then quickly see what the locus is when the initial circles are dis-joint.

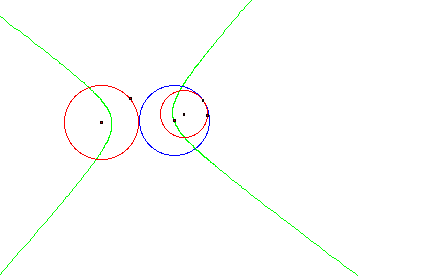
Here we can see the locus is a hyperbola again seeming to have foci at the centers of the initial circles.

Using a piece of technology like GSP encourages creative thinking and a curiosity to explore new ideas by limiting the amount of time the student spends to mechanically construct those ideas. It diminishes the chance that a student will get frustrated at exploring an idea that ultimately does not work out and then give up on trying another idea they may have.