
Exploring Linear Equations whose Product
is a Parabola
by
Julia Neal
The Problem: to find two linear functions
f(x) and g(x) such that their product
h(x) = f(x)*g(x)
is tangent to each of f(x) and g(x)
at two distinct points.
The first step was to explore the product
of two linear functions.
 This graph shows y = 4, y = 2, and
their product y = 8.
Unfortunately, the product of these
functions is not a parabola. It is a linear equation, so we need
be more judicious as to our choice of the two linear functions.
It would be more efficient to choose two linear functions whose
product IS a parabola. So, let's take a look at the equation for
the graph of a parabola,
This graph shows y = 4, y = 2, and
their product y = 8.
Unfortunately, the product of these
functions is not a parabola. It is a linear equation, so we need
be more judicious as to our choice of the two linear functions.
It would be more efficient to choose two linear functions whose
product IS a parabola. So, let's take a look at the equation for
the graph of a parabola,
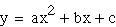 .
Notice in my first example, there was
no x, let alone an x raised to the second power.
In order to acheive x raised to the
second power, each of the two linear functions needs an x. So
let us try y=x +4, y = x+2, and their product, y =(x+4)(2x+2).
.
Notice in my first example, there was
no x, let alone an x raised to the second power.
In order to acheive x raised to the
second power, each of the two linear functions needs an x. So
let us try y=x +4, y = x+2, and their product, y =(x+4)(2x+2).
 Notice, this time we did get a parabola.
Now we can begin to focus more on the way the lines intersect
the parabola. We know that the lines will intersect the parabola
at the parabola's ROOTS, or x intercepts, since the parabola is
written as their product. We may wish to focus on the roots as
we further this investigation. While we would also like the lines
to be tangent to the parabola, we can tell that we have not achieved
this yet because the red line (y=x+4) hits the parabola twice.
Notice, this time we did get a parabola.
Now we can begin to focus more on the way the lines intersect
the parabola. We know that the lines will intersect the parabola
at the parabola's ROOTS, or x intercepts, since the parabola is
written as their product. We may wish to focus on the roots as
we further this investigation. While we would also like the lines
to be tangent to the parabola, we can tell that we have not achieved
this yet because the red line (y=x+4) hits the parabola twice.
 With our next try using the equations
y=x =4, y = -x+2, and y=(x+4)(-x+2), we again notice the intersections
at the roots, but we are no closer to tangency. We need to try
to move the parabola down.
With our next try using the equations
y=x =4, y = -x+2, and y=(x+4)(-x+2), we again notice the intersections
at the roots, but we are no closer to tangency. We need to try
to move the parabola down.
 With this fourth try using the equations
y=x-2, y=-x+2, and y=(x-2)(-x+2) we have come much closer. Unfortunately,
we have only one root. It looks like the parabola will need two
distinct roots, to achieve tangency.
With this fourth try using the equations
y=x-2, y=-x+2, and y=(x-2)(-x+2) we have come much closer. Unfortunately,
we have only one root. It looks like the parabola will need two
distinct roots, to achieve tangency.
 With these equations, y=x-3, y=-x+5
, and y=(x-3)(-x+5), we do not seem to have made much progress,
but comparing these last two graphs, notice that the vertex of
the parabola is the same as the point of intersection of the two
lines. We want the eliminate the second point of interection with
the parabola which happens to be the point of intersection of
the lines as well. We want to move the point of intersection ABOVE
the vertex of the parabola. This would move the graph of the parabola
down a little further, eliminating any extra points of intersection
between the lines and the parabola.
To accomplish this, we need to decrease
the distance between the two roots. In this example, the roots
are 2 units apart. Lets try to get the roots only one unit apart.
To do this we need to look at the difference of the xintercepts
of the linear equations, .
So, let's try y=x-3, y=-x+4, and y=(x-3)(-x+4)
With these equations, y=x-3, y=-x+5
, and y=(x-3)(-x+5), we do not seem to have made much progress,
but comparing these last two graphs, notice that the vertex of
the parabola is the same as the point of intersection of the two
lines. We want the eliminate the second point of interection with
the parabola which happens to be the point of intersection of
the lines as well. We want to move the point of intersection ABOVE
the vertex of the parabola. This would move the graph of the parabola
down a little further, eliminating any extra points of intersection
between the lines and the parabola.
To accomplish this, we need to decrease
the distance between the two roots. In this example, the roots
are 2 units apart. Lets try to get the roots only one unit apart.
To do this we need to look at the difference of the xintercepts
of the linear equations, .
So, let's try y=x-3, y=-x+4, and y=(x-3)(-x+4)
 Success! The lines are tangent to the
parabola.
We have discovered that in order for
the two linear equations to intersect such that they will be tangent
to the parabola which is their product, the lines must :
have slopes with the same magniude
but different directions and
have x intercepts that are 1 unit apart.
Success! The lines are tangent to the
parabola.
We have discovered that in order for
the two linear equations to intersect such that they will be tangent
to the parabola which is their product, the lines must :
have slopes with the same magniude
but different directions and
have x intercepts that are 1 unit apart.
Return to Julia's
mainpage







