

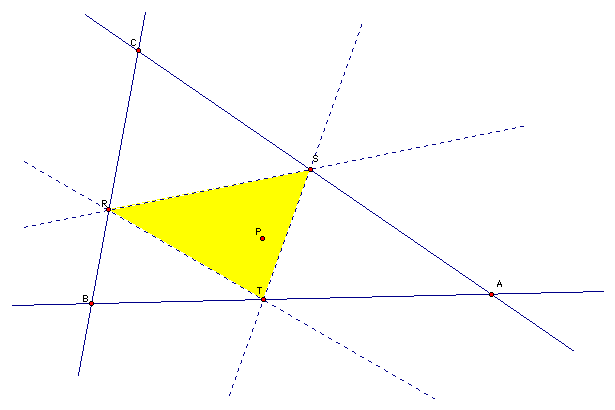
Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
Click here to open a GSP sketch that has a tool to create the pedal triangle for any triangle and point.
Now, let's look at different cases where the pedal point is one of the centers of the original triangle.
Click here for an investigation where the pedal point is the Centroid.
Click here for an investigation where the pedal point is the Incenter.
Click here for an investigation where the pedal point is the Othocenter.
Click here for an investigation where the pedal point is the Circumcenter.
Click here to return to Julie's main page.