Let's investigate
let's look at the effect n has on the graph.
This
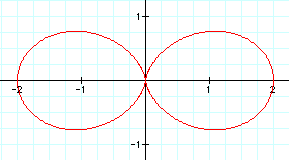
is the case where a = 1, b = 1, and n = 2
This
is the case where a = 1, b = 1, and n = 3.
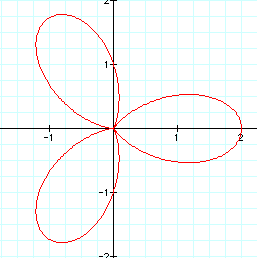
When n>1, the graph is called an "n-leaf rose." The graph is so dubbed because it resembles a flower with a certain number of "petals" equal to the number n. This will also be the case for negative values of n, because of the nature of the cosine function.
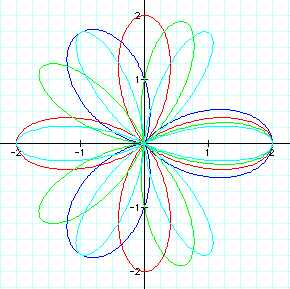
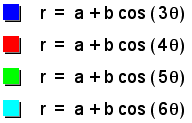
Click here to proceed to a discussion of the effects of n, when n is a fraction.
Click here to proceed to a discussion of the effects of n, when n = 1.
Below are links for the discussions of the effects of the variables a and b on the graph.
Click here for a discussion of the effect a has on the graph.
Click here
for a discussion of the graph of 
Click here to proceed to a discussion of the effect b has on the graph.
An extension to this investigation would be to explore the effects of a, b, and n, when the cosine function is replaced by the sine function.
Click here to return to Julie's main page.