
Some Different Ways to Examine
ax^2 + bx + c =0
by
James W. Wilson and Rives Poe
University of Georgia
It has now become a
rather standard exercise, with availble technology, to construct
graphs to consider the equation
ax^2 + bx + c =0
and to overlay several
graphs of
y = ax^2 + bx + c
for different values
of a, b, or c as the other two are held constant. From these graphs
discussion of the patterns for the roots of
ax^2 + bx + c =0
can be followed.
There are three different outcomes
for the roots of this problem: you will either have no real roots,
one real root, or two real roots.
To understand how a,
b, and c effect the roots of the equation above, we will use the
quadratic formula.
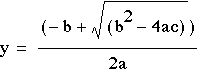 and
and 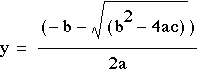 .
To obtain information
about the roots, we need to look at the discriminant. The discriminant
is the part of the formula under the radical sign, (b^2-4ac).
The standard rule for determining roots is as follows: if the
discriminant is positive, there will be two real roots, if the
discriminant equals zero, there will be one real root and if the
discriminant is negative there will be no real roots.
To help students visually
understand this rule and see why it works, use a graphing tool,
such as Graping Calculator. Graph the equation in the xb plane,
where the x-axis represents the x value and the y-axis will represent
the b value. Therefore we will actually use the equation:
.
To obtain information
about the roots, we need to look at the discriminant. The discriminant
is the part of the formula under the radical sign, (b^2-4ac).
The standard rule for determining roots is as follows: if the
discriminant is positive, there will be two real roots, if the
discriminant equals zero, there will be one real root and if the
discriminant is negative there will be no real roots.
To help students visually
understand this rule and see why it works, use a graphing tool,
such as Graping Calculator. Graph the equation in the xb plane,
where the x-axis represents the x value and the y-axis will represent
the b value. Therefore we will actually use the equation:
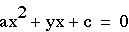 So, let's begin our
exploration to see if we can use the coefficients a and c to predict
the roots of a parabola.
So, let's begin our
exploration to see if we can use the coefficients a and c to predict
the roots of a parabola.
If a and c are both
positive, let a =1 and c =2, then our equation and graph look
like:
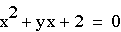
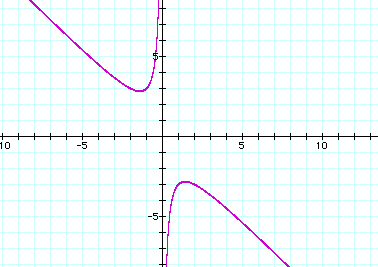 If you will remember
earlier when we discussed the "root" rules of algebra
and the discriminant, it seems that for the graph to have two
real roots then,
If you will remember
earlier when we discussed the "root" rules of algebra
and the discriminant, it seems that for the graph to have two
real roots then, 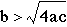 or
or
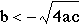 . On the graph above, it looks
like b must be greater thanapproximately 2.8 to have two real
roots or less than -2.8(approximately) to have two real roots.
If we take any particular
value of b, say b=6, and overlay this equation of the
graph we add a line parallel to the x-axis. If it intersects the
curve in the xb plane the intersection points correspond to the
original equation for that value of b. The following graph shows
this intersection.
. On the graph above, it looks
like b must be greater thanapproximately 2.8 to have two real
roots or less than -2.8(approximately) to have two real roots.
If we take any particular
value of b, say b=6, and overlay this equation of the
graph we add a line parallel to the x-axis. If it intersects the
curve in the xb plane the intersection points correspond to the
original equation for that value of b. The following graph shows
this intersection.
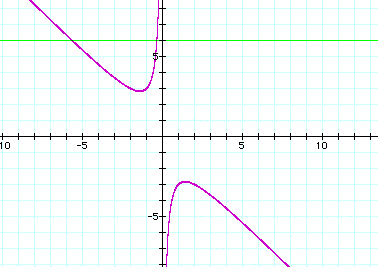 b=6 intersects the
curve in two places, corresponding to the two real roots at x=
-5.64575 and x=-0.354249. There will also be roots if b is less
than -4, as stated earlier, if the line crosses the curve in the
xb plane, the intersection points correspond to the roots of the
original equationfor that value of b. Take a look at b=-5.
b=6 intersects the
curve in two places, corresponding to the two real roots at x=
-5.64575 and x=-0.354249. There will also be roots if b is less
than -4, as stated earlier, if the line crosses the curve in the
xb plane, the intersection points correspond to the roots of the
original equationfor that value of b. Take a look at b=-5.
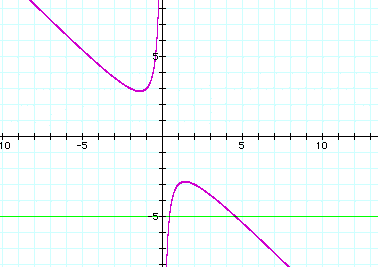 The intersection points,
correspond to the real roots for b=-5 . (x= 0.438447 and x = 4.56155.)
If we plug our values
for a, b and c into the quadratic formula, we get that for the
equation to jave two real roots,
The intersection points,
correspond to the real roots for b=-5 . (x= 0.438447 and x = 4.56155.)
If we plug our values
for a, b and c into the quadratic formula, we get that for the
equation to jave two real roots, 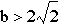 (=2.82843)
and
(=2.82843)
and 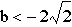 (=-2.82843), which
are the values we determined from the graphs above!
Therefore let b =
(=-2.82843), which
are the values we determined from the graphs above!
Therefore let b =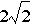 or b=
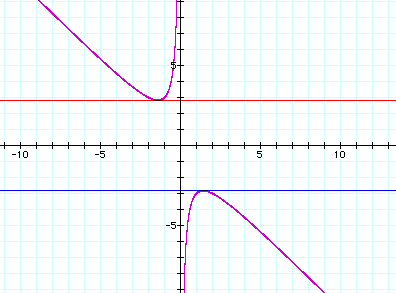
or b=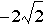 to have one real root as we can see
in the graph below:
to have one real root as we can see
in the graph below:
 And for there to be
no real roots,
And for there to be
no real roots, 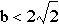 and
and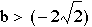 . Which we can see below that there
is no intesection with the curve if we let b = 1 and
b=-1.
. Which we can see below that there
is no intesection with the curve if we let b = 1 and
b=-1.
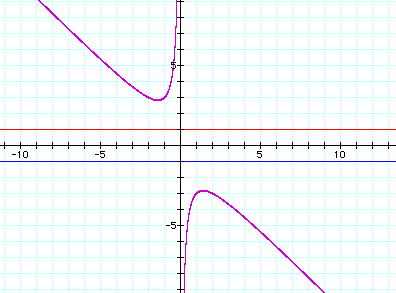
What if both a and
c are negative? Let's investigate this option. Let a = -1and c=-1.
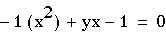
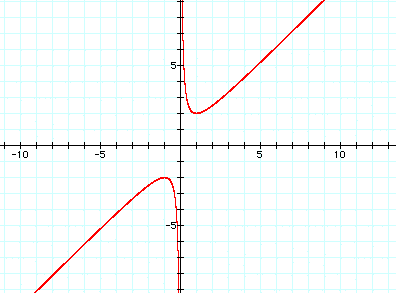 (Notice that this graph
is a reflection over the x-axis of the previous investigation!)
Looking at the graph it seems that b must be greater than 2 or
less than -2, for the equation to have two real roots.
(Notice that this graph
is a reflection over the x-axis of the previous investigation!)
Looking at the graph it seems that b must be greater than 2 or
less than -2, for the equation to have two real roots.
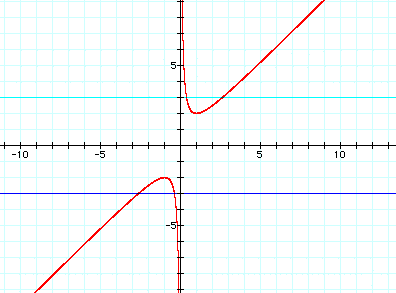 b=3, b=-3
The
real roots if b=3, are x=0.381966 and
x = 2.61803. And if
b=-3, the
real roots are: x=-2.61803 and -0.381966.
According
to the rules of roots, we know that when
b=3, b=-3
The
real roots if b=3, are x=0.381966 and
x = 2.61803. And if
b=-3, the
real roots are: x=-2.61803 and -0.381966.
According
to the rules of roots, we know that when 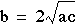 or when
or when 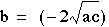 , we will only have
one real root.
, we will only have
one real root.
 b=2,
b=-2
And
according to the third algebraic rule of roots, if
b=2,
b=-2
And
according to the third algebraic rule of roots, if 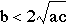 and
and 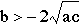 then there will
be no real roots.
then there will
be no real roots.
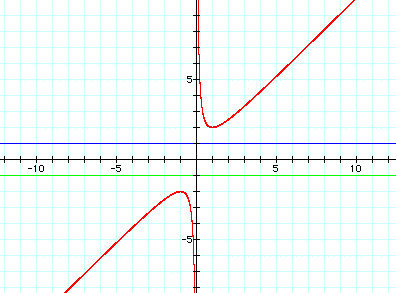 b=1,
b=-1
Onve
again, we are able to show the algebraic rules in graph form.
So far, so good!
b=1,
b=-1
Onve
again, we are able to show the algebraic rules in graph form.
So far, so good!
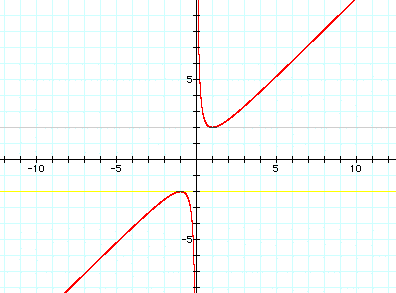
We
need to investigate the third scenario that a and c have different
signs. Let's allow a to equal 1 and c to equal -1.
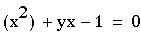
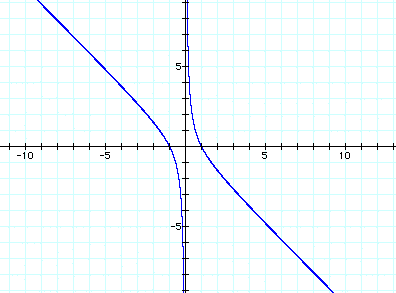 The graph looks a bit
different here, but it is actually easier to see that there are
going to always be two roots in this case. For example, if we
let b = 5 and b=-7:
The graph looks a bit
different here, but it is actually easier to see that there are
going to always be two roots in this case. For example, if we
let b = 5 and b=-7:
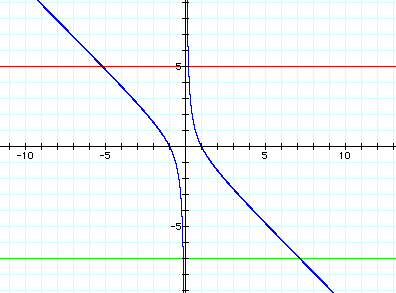 b=5, b=-7
This
can be proved by looking at the discriminant. If a and c have
different signs, then -4ac will always be positive. Also, since
b is squared, b will always be positive, so there will always
be two solutions.
This
ends the investigation of the xb plane and how a and c effect
the roots of an equations such as
ax^2 + bx + c =0.
Using technology is
an excellent way to grasp your students attention and SHOW them
what is happening and how rules came to be!
b=5, b=-7
This
can be proved by looking at the discriminant. If a and c have
different signs, then -4ac will always be positive. Also, since
b is squared, b will always be positive, so there will always
be two solutions.
This
ends the investigation of the xb plane and how a and c effect
the roots of an equations such as
ax^2 + bx + c =0.
Using technology is
an excellent way to grasp your students attention and SHOW them
what is happening and how rules came to be!
Return to home page


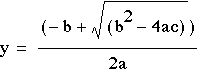 and
and 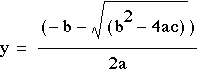 .
.





 b=3, b=-3
b=3, b=-3 b=2,
b=-2
b=2,
b=-2 b=1,
b=-1
b=1,
b=-1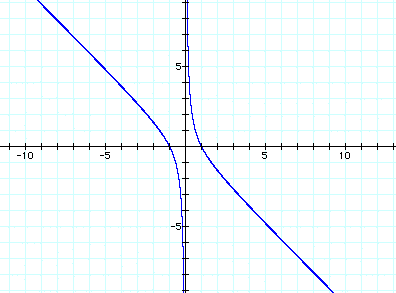
 b=5, b=-7
b=5, b=-7