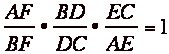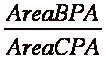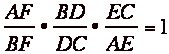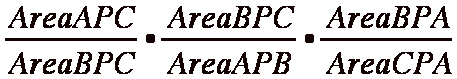Exploring Point P
By: Stephen Bismarck
Exploring Point P
By: Stephen Bismarck
Here's a wield relationship that happens
when you pick a point inside any triangle.
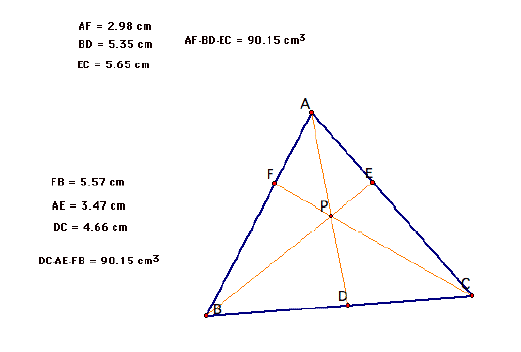 As you can see the product of curtain
sides will give you the same result.
Here's the GSP file to check it out
for yourself.
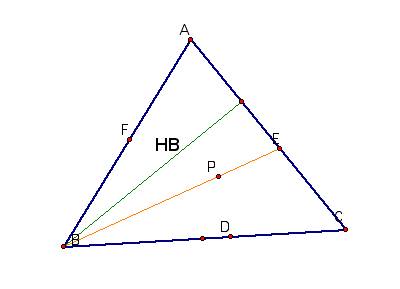
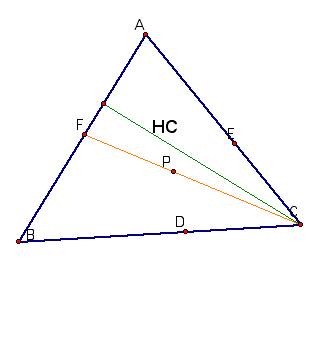
Point P
Basically the relationship is AF*BD*EC
= DC*AE*FB
To make this easier to prove divide
both sides by DC*AE*FB to get
As you can see the product of curtain
sides will give you the same result.
Here's the GSP file to check it out
for yourself.
Point P
Basically the relationship is AF*BD*EC
= DC*AE*FB
To make this easier to prove divide
both sides by DC*AE*FB to get 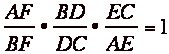 Now to prove that this relationship
is true for all points P and any triangle ABC there's only one
trick
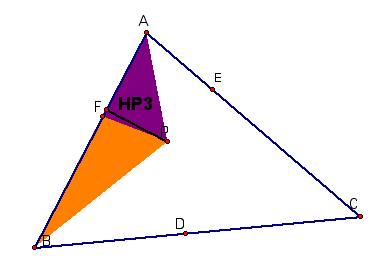
Look at the areas of the triangles
with different bases.
Now to prove that this relationship
is true for all points P and any triangle ABC there's only one
trick
Look at the areas of the triangles
with different bases.
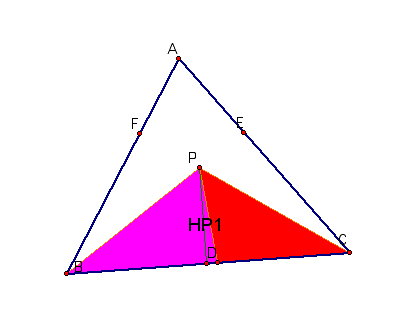
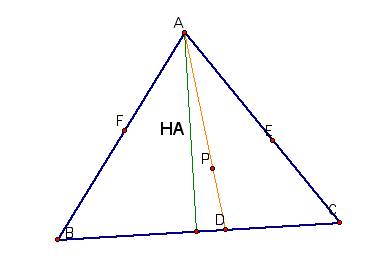 I have added the altitude HA to show
that triangle ABD and triangle ADC have the same altitude.
So the area of triangle ABD = 1/2*HA*BD
and the area of triangle ADC = 1/2*
HA*DC
Solving for BD and DC you get
BD = 2*area ABD/HA
DC = 2*area ADC/HA
I have added the altitude HA to show
that triangle ABD and triangle ADC have the same altitude.
So the area of triangle ABD = 1/2*HA*BD
and the area of triangle ADC = 1/2*
HA*DC
Solving for BD and DC you get
BD = 2*area ABD/HA
DC = 2*area ADC/HA
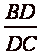

There are more triangles with those
bases
 Using the same procedure of finding
the area and solving for DB and BC you get
Using the same procedure of finding
the area and solving for DB and BC you get
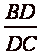

 Since the ratio of those two areas
are equal then they also equal
Since the ratio of those two areas
are equal then they also equal
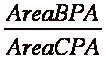
Doing this process for the other triangles
you get
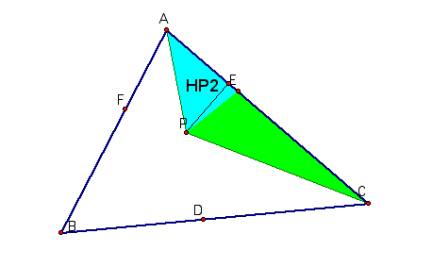
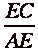
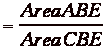
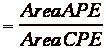

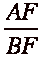



By substituting everything in to the
original equation 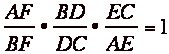
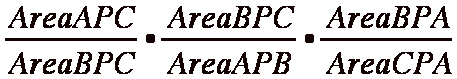 which is equal to 1
Return
which is equal to 1
Return