Lisa Brock

Assignment 1

Examining the Curve y = a sin(bx+c)

Examine the curve y = a sin(bx+c) for different values of a, b, and c.

Let's start by looking at the graph of y = sin x.

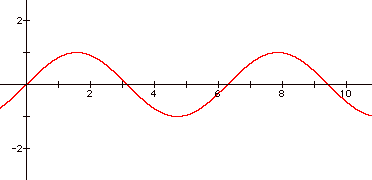
Now, let's look at y = a sin x. Begin by comparing the graph of y = sin x to graphs of y = a sin x when a is a positive number.

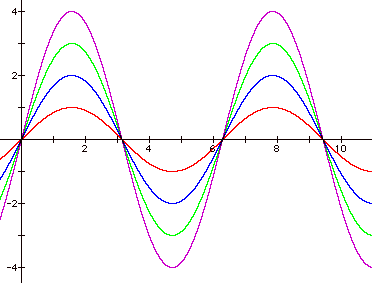
Each curve crosses the x-axis at the same points as y = sin x. As a increases, the distance from the x-axis to each peak or valley increases from 1 unit to a units.

Now let's compare the graph of y = sin x to graphs of y = a sin x when a is a negative number.

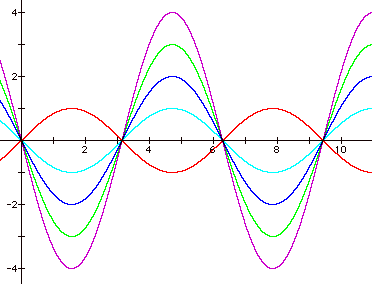
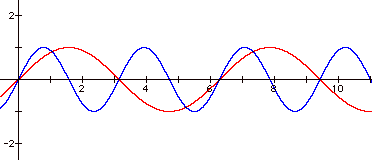
Each curve still crosses the x-axis at the same points as y = sin x. As the absolute value of a increases, the distance from the x-axis to each peak or valley increases. These characteristics are the same as the ones apparent for positive values of a. The negative values of a have an additional affect on the graph. The peaks and valleys are on the opposite side of the x-axis compared to the graph of y = sin x. y = -sin x appears to be the reflection of y = sin x. y = -2sin x appears to be the reflection of y = 2sin x, and so on.

Therefore, a changes the distance between the peak/valley and the x-axis from 1 unit to a units. A negative value of a will also reflect the graph over the x-axis.

Now, let's look at y = sin bx. Begin by comparing the graph of y = sin x to graphs of y = sin bx when b is a positive integer.

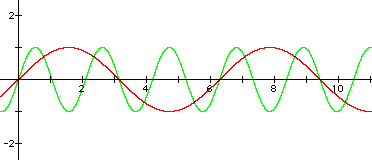
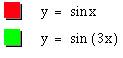
The distance from the peaks and valleys to the x-axis is the same for y = sin x and y = sin(bx). The period of y = sin x is 2p (a complete cycle from the origin, up to the first peak, down to the first valley, and back to the x-axis). The period of y = sin (2x) is p or (2p)/2. The period of y = sin (3x) is (2p)/3. A positive values for b changes the period of the graph to (2p)/b.

Therefore, if b = 1/2, the period of the graph y = sin (1/2 x) is 4p. Let's look at the graph to see if that is the case.

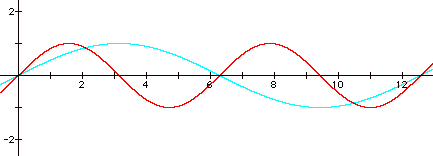
The period of y = sin (1/2 x) is 4p.

Now, let's compare the graph of y = sin x to y = sin (bx) when b is a negative number.

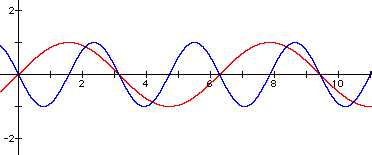
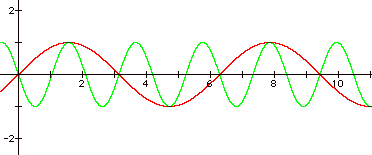
The distance from each peak/valley is still the same as the graph of y = sin x. The period of the graph of y = sin (bx) is still (2p)/b. These characteristics are the same as the ones apparent for positive values of b. The negative values of a have an additional affect on the graph. One cycle of y = sin x begins with a peak and ends with a valley, whereas one cycle of y = sin (bx) begins with a valley and ends with a peak. The graph of y = sin (-2x) is the reflection of y = sin (2x) over the x-axis. The graph of y = sin (-3x) is the reflection of y = sin (3x) over the x-axis, and so on.

Therefore, b changes the period of the graph from 2p to (2p)/b. A negative b also reflects the graph over the x-axis.

Now, let's look at y = sin (x+c). Begin by comparing the graph of y = sin x to graphs of y = sin (x+c) for both positive and negative values of c.

Positive Values of c

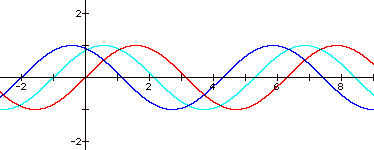
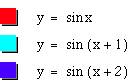
Negative Values of c

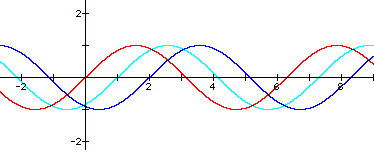
When c is positive, the graph shifts c units to the left. When c is negative, the graph shifts c units to the right.

Now that we know the effect that a, b, and c have on the graph of y = sin x, we can predict the appearance of the graph y = a sin (bx+c).

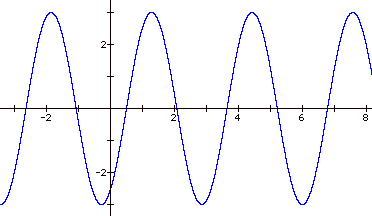
For example, let's take the graph of y = 3 sin (2x-1). The peaks/valleys will be 3 units from the x-axis, the period will be p, and the graph will be shifted 1 unit to the right. Let's graph y = 3 sin (2x-1) to check.

Return to Lisa Brock's Home Page