
Lisa Brock
Assignment 8
The Relationship Between the
Incircle, Nine-Point Circle, and Three Excircles of a Triangle
Is there a relationship between
the incircle, the nine-point circle, and the three excircles of a
triangle? Lets sketch it and see.
Construct any triangle
ABC. Use lines to connect A, B,
and C instead of segments. Then
construct segments connecting A, B, and C. This construction will require both. The incenter, I, is the intersection of
the interior angle bisectors of triangle ABC. Construct I.
Highlight one side of the triangle and point I. Construct a perpendicular line. Create the intersection of the
perpendicular line and the side you highlighted. Highlight, in order, point I and the intersection you just
created. Construct a circle by
center and point. This is the
incircle. Hide the perpendicular
line, the angle bisectors, and the intersection point. Your sketch should look like this:
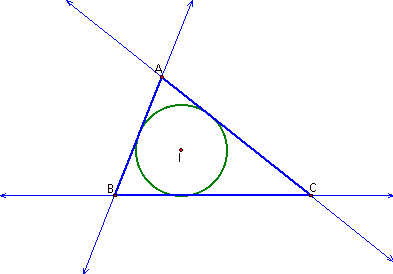
Now lets create the three
excircles. Place a point on each
line extension. Construct the
exterior angle bisectors for a particular side of the triangle. For example, choose side AC. Construct the exterior angle bisector
of the angles with vertex A and vertex C.
Construct the intersection of the two bisectors. This is one excenter. Highlight the excenter and the line
through AC. Construct a
perpendicular line. Construct the
intersection of the perpendicular line and AC. Highlight, in order, the excenter and the intersection
point. Construct a circle by
center and point. This is one
excircle. Repeat this process for
sides AB and BC. Hide the angle
bisectors, perpendicular lines, intersections, and the points on the line
extensions. Your sketch should
look like this:
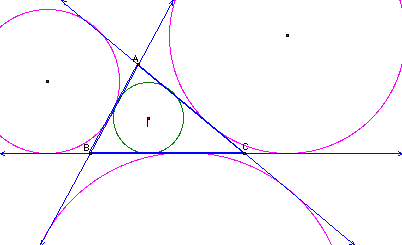
Now lets construct the
nine-point circle. The nine points
consist of the feet of the three altitudes, the midpoints of the segments
connecting each vertex to the orthocenter, and the midpoints of each side. The center of the nine-point circle is
the midpoint of the Euler line, which connects the orthocenter and the
circumcenter.
Let begin by constructing
the orthocenter, H. Construct the
three altitudes. Construct the
intersection of each altitude with the side of the triangle. The intersection of the altitudes is
the orthocenter. Mark it H. Construct a segment from each vertex to
H. Construct the midpoints of each
of these three segments. Hide the
altitudes and the segments from the vertices to H. Construct the midpoint of each side of the triangle. Construct the perpendicular to each
side through each midpoint. The
intersection of these perpendiculars is the circumcenter. Mark it C. Hide the perpendicular lines. Construct the segment connecting H and C. Construct its midpoint. Mark it M. This is the center of the nine-point circle. Hide point H, point C, and the segment
connecting them. Highlight, in
order, point M and one of the nine points on the nine-point circle. Construct a circle by center and
point. Your sketch should look
like this:
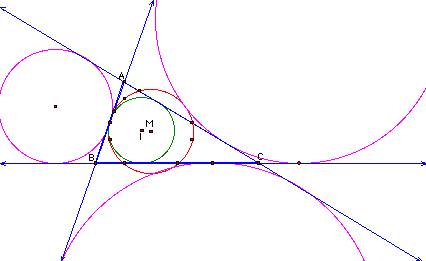
So what is the
relationship? The three excircles
and the incircle are all tangent to the nine-point circle. The incircle is inside of the
nine-point circle. The three
excircles are outside of the nine-point circle. Is this always the case? Click HERE for a GSP sketch that you can move.
Yes, this is always the
case.
Return to Lisa
Brock’s Home Page