
Lisa Brock
Final Assignment
Ceva’s Theorem
Consider any triangle
ABC. Select point P inside the
triangle. Draw lines from A, B,
and C through P. Let points D, E, and
F be the intersections with the opposite side of the triangle.
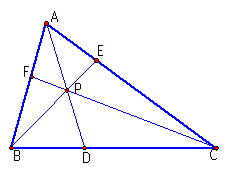
Explore (AF)(BD)(CE) and
(BF)(CD)(AE) for various triangles.
Click HERE to open a GSP sketch. Move P around inside the triangle. Also, move the vertices of the triangle around.
Notice that (AF)(BD)(CE)
and (BF)(CD)(AE) are always equal.
Do you think this always going to be true when P is inside of the
triangle?
By Ceva’s Theorem, this will always be the case. For a proof of Ceva’s Theorem,
click HERE.
What if P is outside of
the triangle? Extend the segments
joining A, B, and C into lines.
Move P outside of the triangle.
Click HERE to open a GSP sketch.
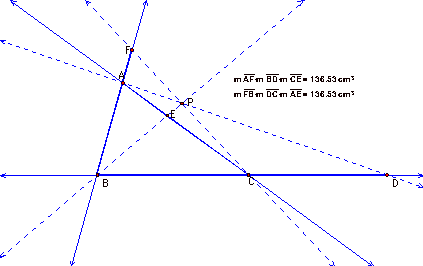
The two products are still
equal! The earlier proof supports
this. Click HERE to view the proof again. Remark 2 of this proof addresses the situation when P is
outside the triangle.
Now lets draw the triangle
DEF. Look at the ratio of the area
of triangle ABC to triangle the area of triangle DEF when P is inside the
triangle. Click HERE to
open a GSP sketch.
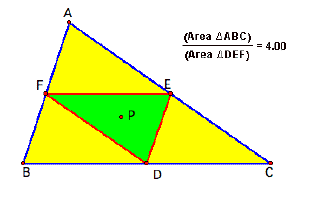
You should have noticed
that the ratio of the areas is always greater than or equal to 4. This can be proven using Routh’s Theorem. This
theorem gives a formula for the area of triangle DEF. The formula is
where l, m, n are the ratios ![]() ,respectively.
,respectively.
Rearranging this equation
gives us a formula for the ratio of the areas of the two triangles.
We have already shown that
lmn=1, so lmn+1=2.
The equation now looks like this:
![]()
(l+1)(m+1)(n+1) has a minimum
value of 8. This occurs when l,m,n=1.
When l,m,n=1,
triangle DEF is the medial triangle.
Since (l+1)(m+1)(n+1) has a minimum value of 8, the ratio of the areas has a minimum
value of 4.
In conclusion, when P is
inside the triangle, the ratio of the area of triangle ABC to the area of
triangle DEF is at least 4, with a minimum value of 4 occurring when triangle
DEF is the medial triangle of triangle ABC.
Return to Lisa Brock’s Home Page