

Objective: Deduce
information about segments and angles after proving that two triangles
are congruent.
In order to prove two segments or two angles congruent:
1. Identify two triangles in which the two segments or angles are corresponding parts.
2. Prove that the triangles are congruent.
3. State that the two pairs are congruent,
using the reason Corr.parts of congruent triangles are congruent.
CPCTC
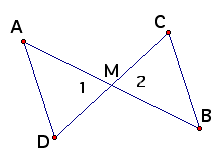
Example 1
Given: Segments AB and CD bisect each other at M
Prove: Segments AD and BC are parallel
Open the figure in gsp and investigate.
Plan for Proof: You can prove AD is parallel to BC if you can show that alternate interior angles A and B are congruent. You will know that angle A and angle B are congruent if they are corresponding parts of congruent triangles. The diagram suggests that you try to prove triangle AMB is congruent to triangle BMC.
| Statements | Reasons |
| 1. Given | 1. Given |
| 2. M is the midpoint of AB and of CD | 2. Def of a bisector of a segment |
| 3. AM is congruent to MB; DM is congruent to MC | 3. Def. of midpoint |
| 4. Angle AMD congr. angle BMC | 4. Vertical angles are congruent. |
| 5. Triangle AMD congr. to triangle BMC | 5. SAS Postulate |
| 6. Angle A is congr. to angle B | 6. Corr parts of congr. triangles are congr. |
| 7. AD is parallel to BC | 7. If two lines are cut by a transversal and alt. int. angles are congr., then lines are parallel. |
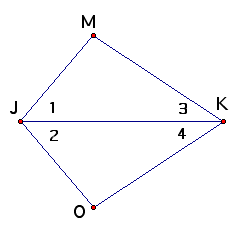
Example 2
Given: Segment MK is congruent to segment OK
Segment KJ bisects angle MKO
Prove: Segment JK bisects angle MJO
Open the figure in gsp and investigate.
| Statements | Reasons |
| 1. | 1. Given |
| 2. | 2. Given |
| 3. | 3. |
| 4. | 4. |
| 5. | 5. SAS postulate |
| 6. | 6. |
| 7. | 7. Def. of angle bisector |
Exercises (write proofs using 2 column form)
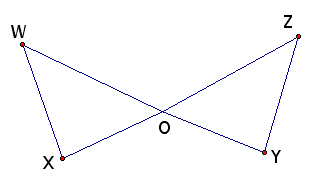
1. Given: Segment WO congr. ZO; XO congr. YO
Prove: Angle W congr. Angle Z.
2. Given: M is the midpoint of AB
Prove: AC congr. BD

3. Given: AD // ME; MD // BE; M is the midpoint of AB
Prove: MD congr. BE

4. Given: M is the midpoint of AB; AD congr. ME; AD // ME
Prove: MD // BE