

Objective: Identify
corresponding parts of congruent figures.
Definition: Two geometric figures are congruent if they have exactly the same size and shape.
Congruent
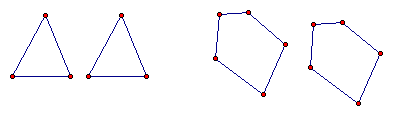
Not Congruent
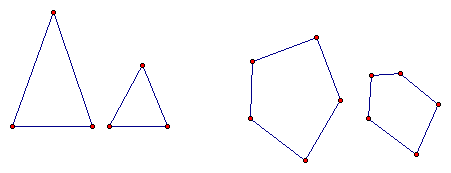
When two figures are congruent there is a correspondence between their angles and sides.
Corresponding angles are congruent.
AND
Corresponding sides are congruent.

In the figure above, triangle ABC is congruent to triangle FDE. Angle A is congruent to angle F, angle B is congruent to angle D, segment AB is congruent to FD, etc.
Definition: Two triangles are congruent if and only if their vertices can be matched up so that the corresponding parts (angles and sides) of the triangles are congruent. (Same thing is true of polygons.)
Corollary: If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
From the illustration above, if angle A is congruent to angle F and angle B is congruent to angle D, then angle C is congruent to angle E.
Properties of Congruent Triangles
Reflexive Property of Congruent Triangles: Every triangle is congruent to itself.
Symmetric Property of Congruent Triangles: If triangle ABC is congruent to triangle FDE, then triangle FDE is congruent to triangle ABC.
Transitive Property of Congruent Triangles:
If triangle ABC is congruent to triangle
FDE and triangle FDE is congruent to triangle JKL, then triangle
ABC is congruent to triangle JKL.
EXERCISES
Suppose triangle BIG is congruent to triangle CAT. Complete.
1. Angle G is congruent to....
2. ......= the measurement of angle A.
3. BI = ...............
4. ......... is congruent to segment AT.
5. Triangle IGB is congruent to ........
6. ......... is congruent to triangle CTA.
7. If triangle DEF is congruent to triangle RST, and the measurement of angle D=100 and angle F=40, name four congruent angles.
8. Suppose triangle LXR is congruent to triangle FNE. List six congruences that can be justified by the following reason: Corr. parts of congruent triangles are congruent.