

Have students complete this activity using Geometer's Sketchpad.
I. Medians in a Triangle
1. Construct triangle ABC.
2. Construct the midpoints of the 3 sides.
3. Construct 2 of the 3 medians, each connecting a vertex with the midpoint of its opposite side.
4. Construct the point of intersection of the two medians.
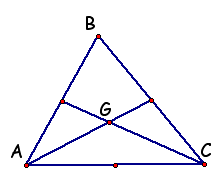
5. Construct the third median.
Question 1: What do you notice about this third median? Drag a vertex of the triangle to confirm that this conjecture holds for any triangle.
6. The point where the medians intersect is called the centroid. Show its label and change it to Ce for centroid.

7. Measure the distance from B to Ce and the distance from Ce to the midpoint F.
8. Drag vertices of triangle ABC and look for a relationship between BCe and CeF.
9. Make a table with these two measures.
10. Change the triangle and double-click on the table values to add another entry.
11. Keep changing the triangle and adding entries to your table until you can see a relationship between the distances BCe and CeF.
Question 2: Write a conjecture about the way the centroid divides each median in a triangle.
II. Altitudes in a Triangle
1. Construct triangle ABC.
2. Construct a line perpendicular to AC through point B.
Question 1: As long as your triangle is acute, this perpendicular line should intersect a side of the triangle. Drag point B so that the line falls outside the triangle. Now what kind of triangle is it?

3. With the perpendicular line outside the triangle, use a line to extend side AC so that it intersects the perpendicular line.
4. Construct point D, the point of intersection of the extended side and the perpendicular line.
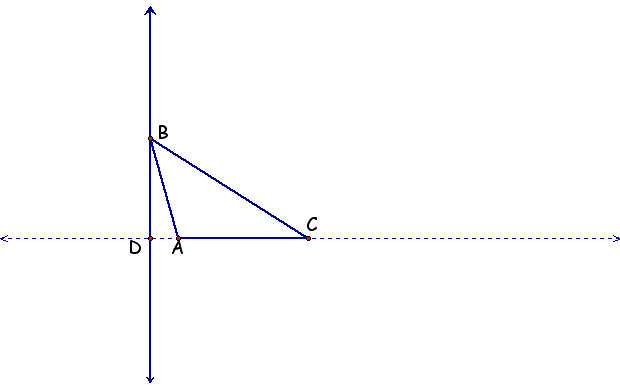
5. Hide the lines.
6. Construct BD. Segment BD is an altitude.
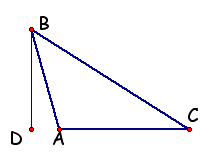
7. Drag vertices of the triangle and observe how your altitude behaves.
Question 2: Where is your altitude when angle A is a right angle?
8. Drag your triangle so that it is acute again(with the altitude falling inside the triangle).
9. Construct the second and third altitudes.

10. Drag the triangle and observe how the 3 altitudes behave.
Question 3: What do you notice about the 3 altitudes when the triangle is acute?
Question 4: What do you notice about the altitudes when the triangle is obtuse?
11. Make sure the triangle is obtuse. Construct 2 lines that each contain an altitude.
12. Construct their point of intersection. This point is called the orthocenter of the triangle.
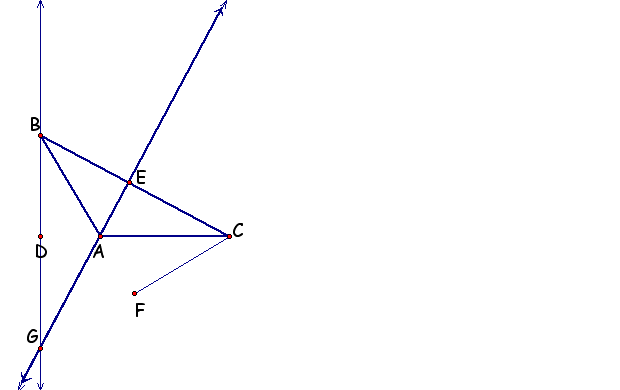
13. Construct a line containing the third altitude.
14. Drag the triangle and observe the lines.
Question 5: What
do you notice about the lines containing the altitudes?
III. Perpendicular Bisectors in a Triangle
1. Construct triangle ABC.
2. Construct the midpoints of the sides.
3. Construct two of the three perpendicular bisectors in the triangle.
4. Construct point G, the point of intersection of these lines.

5. Construct the third perpendicular bisector.
Question 1: What do you notice about this third perpendicular bisector? Drag a vertex of the triangle to confirm that this conjecture holds for any triangle.
6. Drag a vertex around so that point G moves into and out of the triangle. Observe the angles of the triangle as you do this.
Question 2: In what type of triangle is point G outside the triangle? inside the triangle?
Question 3: Drag a vertex until point G falls on a side of the triangle. What kind of triangle is this? Where exactly does point G lie?
7. Measure the distances from point G to each of the 3 vertices.
8. Drag a vertex of the triangle and observe the distances.
Question 4: The point of intersection of the 3 perpendicular bisectors is called the circumcenter of the triangle. What do you notice about the distances from the circumcenter to the 3 vertices of the triangle?
9. Construct a circle with center G and radius endpoint A. This is the circumscribed circle of triangle ABC.

Reference:
Exploring Geometry with the Geometer's Sketchpad by Key Curriculum Press