

Objective: Prove
two triangles congruent by using the SSS, SAS, and the ASA Postulates.
SSS Postulate
If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
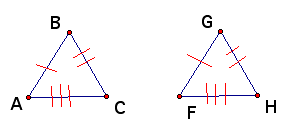
By the SSS Postulate, triangle ABC is congruent to triangle FGH.
SAS Postulate
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.

By the SAS Postulate, triangle ABC is congruent to triangle FGH.
ASA Postulate
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.

By the ASA Postulate, triangle ABC is congruent to triangle FGH.
Proving Triangles Congruent Using the SAS Postulate:
Given: Segment OK bisects angle MOT and segment OM is congruent to OT
Prove: Triangle MOK is congruent to triangle TOK
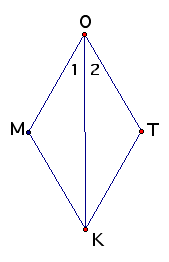
| Statements | Reasons |
| 1. Segment OK bisects angle MOT | 1. Given |
| 2. angle 1 is congruent to angle 2 | 2. Definition of angle bisector |
| 3. Segment OK is congruent to segment OK | 3. Reflexive |
| 4. Segment OM is congruent to segment OT | 4. Given |
| 5. Triangle MOK is congruent to triangle TOK | 5. SAS Postulate |
Proving Triangles Congruent Using the ASA Postulate:
Given: Segment BA is perpendicular to segment YZ and segment BA bisects angle YBZ
Prove: Triangle AYB is congruent to triangle AZB

| Statements | Reasons |
| 1. Segment BA is perpendicular to segmt YZ | 1. Given |
| 2. Angle 1 is congruent to angle 2 | 2. If 2 lines are perpendicular, they form congruent adjacent angles |
| 3. Segment BA bisects angle YBZ | 3. Given |
| 4. Angle 3 is congruent to angle 4 | 4. Def. of angle bisector |
| 5. Segment AB is congruent to segment AB | 5. Reflexive |
| 6. Triangle AYB is congruent to triang AZB | 6. ASA Postulate |
Exercises
Supply the missing reasons.
1. Given: Segment AB is parallel to segment DC; Segment AB is congruent to segment DC
Prove: Triangle ABC is congruent to triangle CDA

| Statements | Reasons |
| 1. Segment AB is congruent to segment DC | 1. ? |
| 2. Segment AC is congruent to segment AC | 2. ? |
| 3. Segment AB is parallel to segment DC | 3. ? |
| 4. Angle BAC is congruent to angle DCA | 4. ? |
| 5. Triangle ABC is congruent to triangle CDA | 5 ? |
2. Given: Segment RS is perpendicular to segment ST; Segment TU is perpendicular to segment ST; V is the midpoint of segment ST.
Prove: Triangle RSV is congruent to triangle UTV.

| Statements | Reasons |
| 1. Segment RS is perpend to ST; Segment TU is perpend to ST | 1. ? |
| 2. Angle S =90; Angle ? =90 | 2. ? |
| 3. Angle S is congruent to Angle T | 3. ? |
| 4. V is the midpoint of ST | 4. ? |
| 5. Segment SV is congruent to ? | 5. ? |
| 6. Angle RVS is congruent to angle ? | 6. ? |
| 7. Triangle ? is congruent to triangle ? | 7. ? |
Write proofs in two-column form.

3. Given: Segment TM is congruent to PR; Segment TM is parallel to RP
Prove: Triangle TEM is congruent to triangle PER
4. Given: E is the midpoint of segment TP; E is the midpoint of segment M
Prove: Triangle TEM is congruent to triangle PER