Objective: Prove two triangles congruent by first proving two other triangles are congruent.
*Sometimes two triangles that we want to prove congruent have common parts with two other triangles that we can easily prove congruent. We may then be able to use corresponding parts of these other triangles to prove the original triangles congruent.
Example:
Given: Angle 1 congruent to Angle 2; Angle 5 congruent to Angle 6
Prove: AC perpendicular to BD

Plan for Proof: In this example, it is helpful to reason backward from what you want to prove. We can show AC perpendicular to BD if we can show Angle 3 congruent to Angle 4. We can prove Angle 3 congruent Angle 4 if we can prove that the angles are corresponding parts of congruent triangles. To prove triangle ABO congruent to triangle ADO, we need AB congruent to AD. We can prove this congruence by proving that triangle ABC is congruent to triangle ADC. We should prove this first.
| 1. Angle 1 congruent to Angle 2; Angle 5 congruent to Angle 6 | 1. Given |
| 2. AC congruent to AC | 2. Reflexive |
| 3. Triangle ABC congruent to Triangle ADC | 3. ASA Postulate |
| 4. AB congruent to AD | 4. CPCTC |
| 5. AO congruent to AO | 5. Reflexive |
| 6. Triangle ABO congruent to Triangle ADO | 6. SAS |
| 7. Angle 3 congruent to Angle 4 | 7. CPCTC |
| 8. AC perpendicular to BD | 8. If 2 lines form congruent adjacent angles, then the lines are perpendicular. |
Exercise Proofs
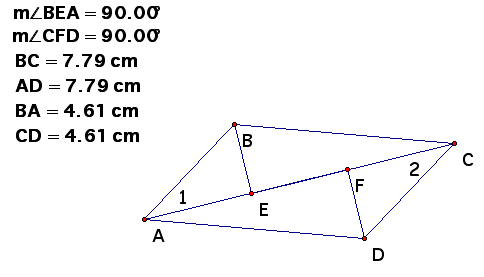
1. Prove: BE congruent to DF
Key steps of proof:
a. Triangle ABC congruent to Triangle CDA
b. Angle 1 congruent to Angle 2
c. Triangle ABE congruent to Triangle CDF
d. BE congruent to DF
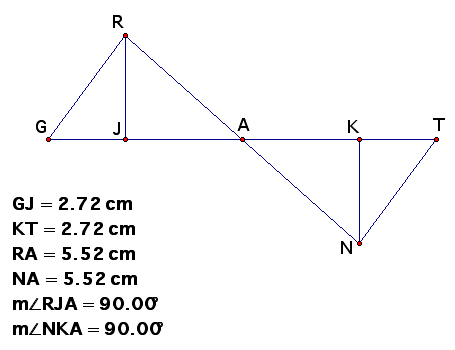
2. Prove: Angle G congruent to Angle T
Key steps of proof:
a. Triangle RAJ congruent to Triangle NAK
b. RJ congruent to NK
c. Triangle GRJ congruent to Triangle TNK
d. Angle G congruent to Angle T