Investigating

Write-up by
Blair T. Dietrich
EMAT 6680

Part I.

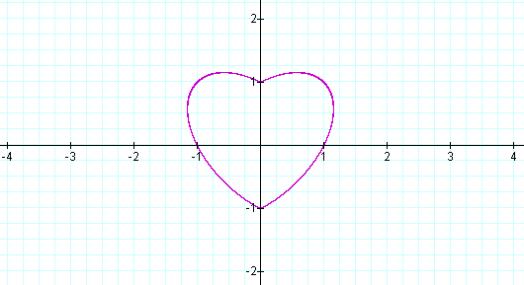
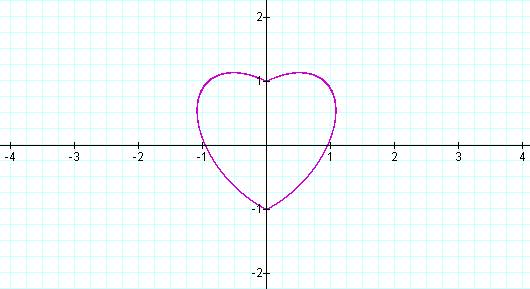
This equation yields some surprising results as the coefficient of y|x| is changed.

When a=1 the graph appears heart-shaped. This is equivalent to the original form of

the equation

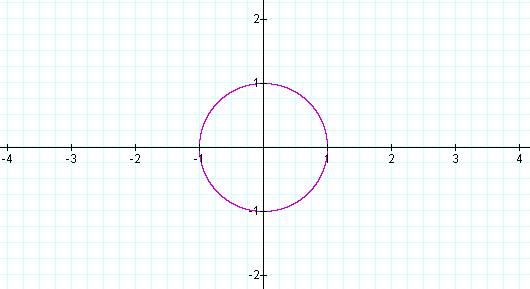
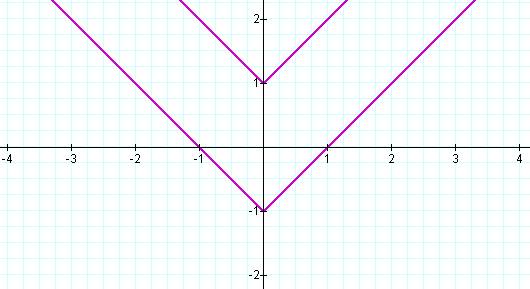
When a=0, the unit circle appears…

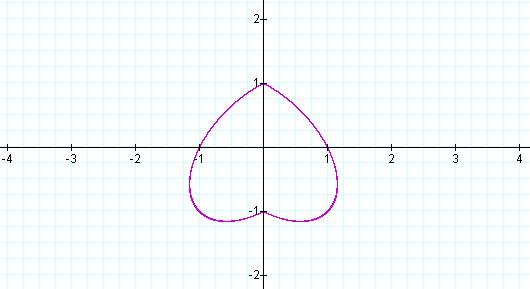
When a= -1, it's an upside-down heart…

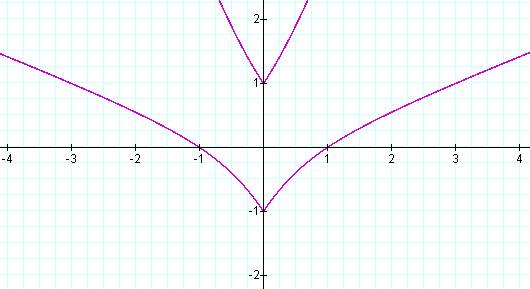
When a = -2, parallel absolute value graphs appear…

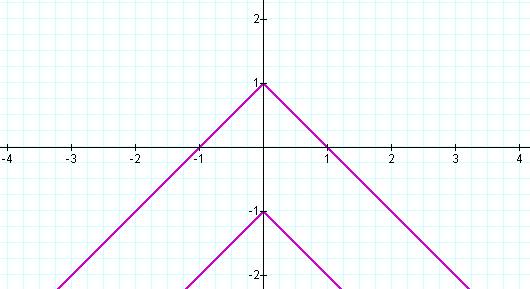
When a = -3, the lines "warp"

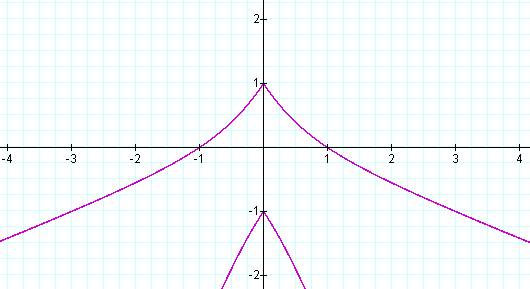
Similarly, when a = 2 and a = 3, respectively, the graph shows parallel absolute value graphs and warped lines in the opposite direction.

Part II.

What if the coefficient of x^2 changes?

Consider the graph of the relation shown below:

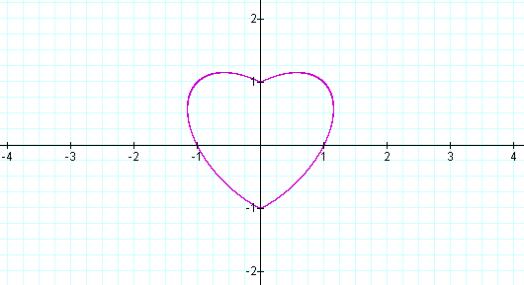
When a = 1, the equation (and, hence, the graph) is the same as that of

As a gets smaller, the heart dilates…(here, a = 0.3)

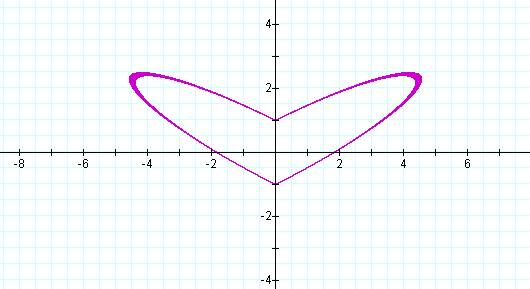
But when a = 0.2, the heart "breaks"…

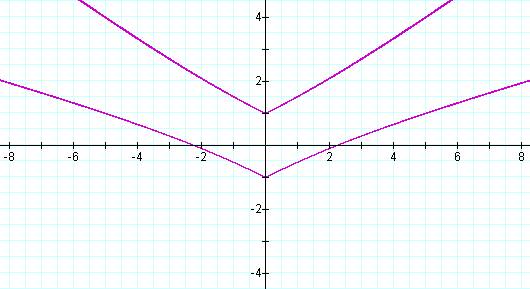
Eventually, the pieces bend away from each other…(a = -3 shown)

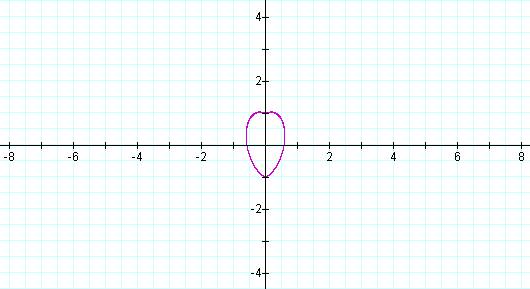
For a > 1, the "heart" just gets more compressed horizontally (a = 3 shown)

III.

Just as easily adjusted is the coefficient of y^2.

Consider the graph of the relation shown below:

Again, when a = 1 the equation (and, hence, the graph) is the same as that of

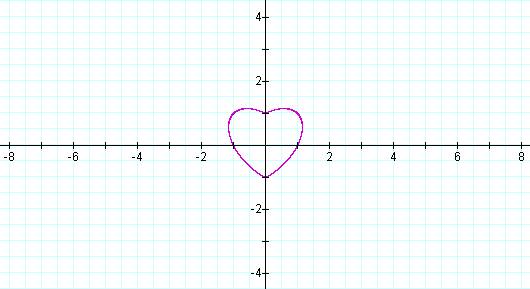
As a gets smaller, the heart dilates before splitting apart:

(a = 0.3)

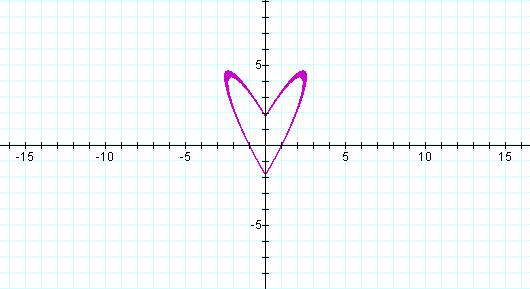
(a=0)

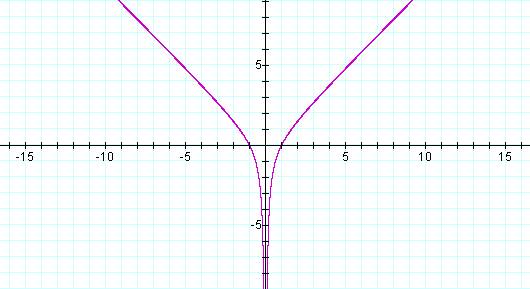
(a = -1)

Return to Blair Dietrich's EMAT 6680 page