Investigating the pattern of
roots
as the linear
coefficient b changes
in the general quadratic
Write-up by
Blair T. Dietrich
EMAT 6680
This investigation will explore the pattern of
roots for the
general quadratic 
. While holding
constant the values of each of a and c at 1, the value
of b
will be allowed to vary.
Consider the
equation 
. Try your own
values of b here.
By overlaying the
graphs for b = -3, -2, -1, 0, 1, 2, 3, the following picture is
obtained:
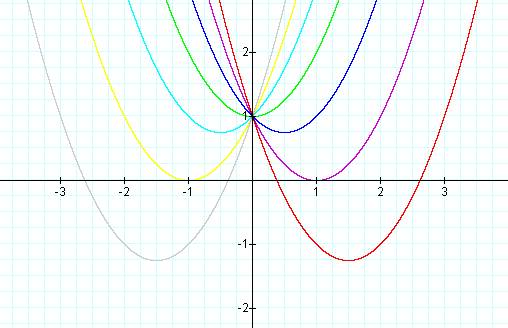
We notice that all of the graphs shown have the
point (0,1)
in common. This is reasonable since c
is fixed at 1 and this corresponds to the y-intercept.
If we were to observe the graph of 
as b varies,
we could try to visualize the movement of the curve along a fixed path
that
would be traced out by the successive vertices of each parabola. This path seems to be symmetric about and
centered at the line x = 0.
In general, we can
determine the vertex of a parabola by finding the axis of symmetry 
for
the general quadratic 
. Specifically, for
quadratics of the form 
,
the line of symmetry is 
. By substitution, we
can find the vertex:
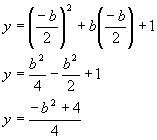
So we find that the vertex will occur at the point
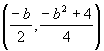for
any given value of b.
Due to the symmetric nature of the path of
vertices the
locus of points is known to also contain the point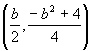 
.
Also, as we have observed, the point (0,1) will also be on this path.
Recall that three points will define a quadratic
equation 
. We know that C = 1
(the y-intercept). We can find the
values of A and B
by solving the following system of equations:
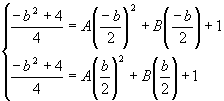
By
substitution,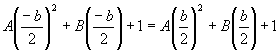 
Since b varies (i.e. not constant) it is not (in general) equal to zero. Therefore, B = 0.
Back-substituting, we can find A:
A = -1
Therefore, the quadratic function that passes
through the
vertices of all parabolas of the form 
is 
. This equation is
shown in black on the graph below:
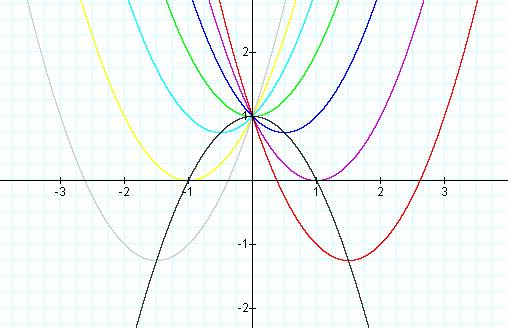
