Assignment #12:

Investigations Using a Spreadsheet

By Amber Krug

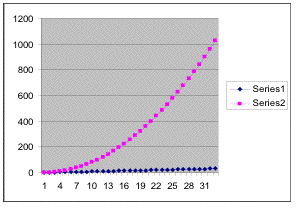
I used the function f(x) = x². The following spreadsheet is the result:

x	y
0	0
1	1
2	4
3	9
4	16
5	25
6	36
7	49
8	64
9	81
10	100
11	121
12	144
13	169
14	196
15	225
16	256
17	289
18	324
19	361
20	400
21	441
22	484
23	529
24	576
25	625
26	676
27	729
28	784
29	841
30	900
31	961
32	1024

We can then graph the data to find the following:

I then investigated the Fibonacci Sequence. The following is a table of the Fibonacci Sequence:

n	*f(n)*	*Ratio of every adjacent term*	*Ratio of every second term*	*Ratio of every third term*	*Ratio of every fourth term*
0	1
1	1	1
2	2	0.5	0.5
3	3	0.666667	0.333333	0.333333
4	5	0.6	0.4	0.2	0.2
5	8	0.625	0.375	0.25	0.125
6	13	0.615385	0.384615	0.230769	0.153846
7	21	0.619048	0.380952	0.238095	0.142857
8	34	0.617647	0.382353	0.235294	0.147059
9	55	0.618182	0.381818	0.236364	0.145455
10	89	0.617978	0.382022	0.235955	0.146067
11	144	0.618056	0.381944	0.236111	0.145833
12	233	0.618026	0.381974	0.236052	0.145923
13	377	0.618037	0.381963	0.236074	0.145889
14	610	0.618033	0.381967	0.236066	0.145902
15	987	0.618034	0.381966	0.236069	0.145897
16	1597	0.618034	0.381966	0.236068	0.145899
17	2584	0.618034	0.381966	0.236068	0.145898
18	4181	0.618034	0.381966	0.236068	0.145898
19	6765	0.618034	0.381966	0.236068	0.145898
20	10946	0.618034	0.381966	0.236068	0.145898
21	17711	0.618034	0.381966	0.236068	0.145898
22	28657	0.618034	0.381966	0.236068	0.145898
23	46368	0.618034	0.381966	0.236068	0.145898
24	75025	0.618034	0.381966	0.236068	0.145898
2 5	121393	0.618034	0.381966	0.236068	0.145898
26	196418	0.618034	0.381966	0.236068	0.145898
27	317811	0.618034	0.381966	0.236068	0.145898
28	514229	0.618034	0.381966	0.236068	0.145898
29	832040	0.618034	0.381966	0.236068	0.145898
30	1346269	0.618034	0.381966	0.236068	0.145898
31	2178309	0.618034	0.381966	0.236068	0.145898
32	3524578	0.618034	0.381966	0.236068	0.145898
33	5702887	0.618034	0.381966	0.236068	0.145898
34	9227465	0.618034	0.381966	0.236068	0.145898

We see that as n increases, the ratio of every adjacent term approaches 0.618034. When we look at the ratio of every second element, the limit approaches 0.381966; the ratio of every third element reaches a limit of 0.236068; the ratio of every fourth element reaches a limit of 0.145898.

If we alter the values of f(n) so that we result in the following:

n	*f(n)*	*Ratio of every adjacent term*	*Ratio of every second term*	*Ratio of every third term*	*Ratio of every fourth term*
0	1
1	2	0.5
2	3	0.666667	0.333333
3	5	0.6	0.4	0.2
4	8	0.625	0.375	0.25	0.125
5	13	0.615385	0.384615	0.230769	0.153846
6	21	0.619048	0.380952	0.238095	0.142857
7	34	0.617647	0.382353	0.235294	0.147059
8	55	0.618182	0.381818	0.236364	0.145455
9	89	0.617978	0.382022	0.235955	0.146067
10	144	0.618056	0.381944	0.236111	0.145833
11	233	0.618026	0.381974	0.236052	0.145923
12	377	0.618037	0.381963	0.236074	0.145889
13	610	0.618033	0.381967	0.236066	0.145902
14	987	0.618034	0.381966	0.236069	0.145897
15	1597	0.618034	0.381966	0.236068	0.145899
16	2584	0.618034	0.381966	0.236068	0.145898
17	4181	0.618034	0.381966	0.236068	0.145898
18	6765	0.618034	0.381966	0.236068	0.145898
19	10946	0.618034	0.381966	0.236068	0.145898
20	17711	0.618034	0.381966	0.236068	0.145898
21	28657	0.618034	0.381966	0.236068	0.145898
22	46368	0.618034	0.381966	0.236068	0.145898
23	75025	0.618034	0.381966	0.236068	0.145898
24	121393	0.618034	0.381966	0.236068	0.145898
25	196418	0.618034	0.381966	0.236068	0.145898
26	317811	0.618034	0.381966	0.236068	0.145898
27	514229	0.618034	0.381966	0.236068	0.145898
28	832040	0.618034	0.381966	0.236068	0.145898
29	1346269	0.618034	0.381966	0.236068	0.145898
30	2178309	0.618034	0.381966	0.236068	0.145898
31	3524578	0.618034	0.381966	0.236068	0.145898
32	5702887	0.618034	0.381966	0.236068	0.145898
33	9227465	0.618034	0.381966	0.236068	0.145898
34	14930352	0.618034	0.381966	0.236068	0.145898

n	*f(n)*	*Ratio of every adjacent term*	*Ratio of every second term*	*Ratio of every third term*	*Ratio of every fourth term*
0	1
1	3	0.333333
2	4	0.75	0.25
3	7	0.571429	0.428571	0.142857
4	11	0.636364	0.363636	0.272727	0.090909
5	18	0.611111	0.388889	0.222222	0.166667
6	29	0.62069	0.37931	0.241379	0.137931
7	47	0.617021	0.382979	0.234043	0.148936
8	76	0.618421	0.381579	0.236842	0.144737
9	123	0.617886	0.382114	0.235772	0.146341
10	199	0.61809	0.38191	0.236181	0.145729
11	322	0.618012	0.381988	0.236025	0.145963
12	521	0.618042	0.381958	0.236084	0.145873
13	843	0.618031	0.381969	0.236062	0.145907
14	1364	0.618035	0.381965	0.23607	0.145894
15	2207	0.618034	0.381966	0.236067	0.145899
16	3571	0.618034	0.381966	0.236068	0.145898
17	5778	0.618034	0.381966	0.236068	0.145898
18	9349	0.618034	0.381966	0.236068	0.145898
19	15127	0.618034	0.381966	0.236068	0.145898
20	24476	0.618034	0.381966	0.236068	0.145898
21	39603	0.618034	0.381966	0.236068	0.145898
22	64079	0.618034	0.381966	0.236068	0.145898
23	103682	0.618034	0.381966	0.236068	0.145898
24	167761	0.618034	0.381966	0.236068	0.145898
25	271443	0.618034	0.381966	0.236068	0.145898
26	439204	0.618034	0.381966	0.236068	0.145898
27	710647	0.618034	0.381966	0.236068	0.145898
28	1149851	0.618034	0.381966	0.236068	0.145898
29	1860498	0.618034	0.381966	0.236068	0.145898
30	3010349	0.618034	0.381966	0.236068	0.145898
31	4870847	0.618034	0.381966	0.236068	0.145898
32	7881196	0.618034	0.381966	0.236068	0.145898
33	12752043	0.618034	0.381966	0.236068	0.145898
34	20633239	0.618034	0.381966	0.236068	0.145898

n	*f(n)*	*Ratio of every adjacent term*	*Ratio of every second term*	*Ratio of every third term*	*Ratio of every fourth term*
0	1
1	4	0.25
2	5	0.8	0.2
3	9	0.555556	0.444444	0.111111
4	14	0.642857	0.357143	0.285714	0.071429
5	23	0.608696	0.391304	0.217391	0.173913
6	37	0.621622	0.378378	0.243243	0.135135
7	60	0.616667	0.383333	0.233333	0.15
8	97	0.618557	0.381443	0.237113	0.14433
9	157	0.617834	0.382166	0.235669	0.146497
10	254	0.61811	0.38189	0.23622	0.145669
11	411	0.618005	0.381995	0.23601	0.145985
12	665	0.618045	0.381955	0.23609	0.145865
13	1076	0.61803	0.38197	0.236059	0.145911
14	1741	0.618036	0.381964	0.236071	0.145893
15	2817	0.618033	0.381967	0.236067	0.1459
16	4558	0.618034	0.381966	0.236068	0.145897
17	7375	0.618034	0.381966	0.236068	0.145898
18	11933	0.618034	0.381966	0.236068	0.145898
19	19308	0.618034	0.381966	0.236068	0.145898
20	31241	0.618034	0.381966	0.236068	0.145898
21	50549	0.618034	0.381966	0.236068	0.145898
22	81790	0.618034	0.381966	0.236068	0.145898
23	132339	0.618034	0.381966	0.236068	0.145898
24	214129	0.618034	0.381966	0.236068	0.145898
25	346468	0.618034	0.381966	0.236068	0.145898
26	560597	0.618034	0.381966	0.236068	0.145898
27	907065	0.618034	0.381966	0.236068	0.145898
28	1467662	0.618034	0.381966	0.236068	0.145898
29	2374727	0.618034	0.381966	0.236068	0.145898
30	3842389	0.618034	0.381966	0.236068	0.145898
31	6217116	0.618034	0.381966	0.236068	0.145898
32	10059505	0.618034	0.381966	0.236068	0.145898
33	16276621	0.618034	0.381966	0.236068	0.145898
34	26336126	0.618034	0.381966	0.236068	0.145898

We find that the limits of the ratios of the adjacent terms, second terms, third terms, and fourth terms all remain the same as our original table.

Return