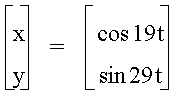__________________________________________
PARAMETRIC
EQUATIONS
By:† Lauren Lee
__________________________________________
†††† A parametric curve in the plane is a pair
of functions
(x = f(t) and y = g(t)),
where the two continuous functions define ordered pairs (x,y). The two
equations are usually called the parametric equations of a curve. The extent of
the curve will depend on the range of t and your work with parametric
equations should pay close attention the range of t.† In many applications, we think of
x and y "varying with time t " or the angle of
rotation that some line makes from an initial location.
________________________________________________________
† Letís look at the
following parametric equations and vary a and b:
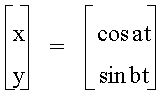
for †0 <
t < 2pi
† What happens when
we set a and b equal?
† Letís look at† a = 2 †and† b = 2
†
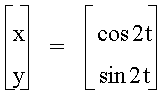
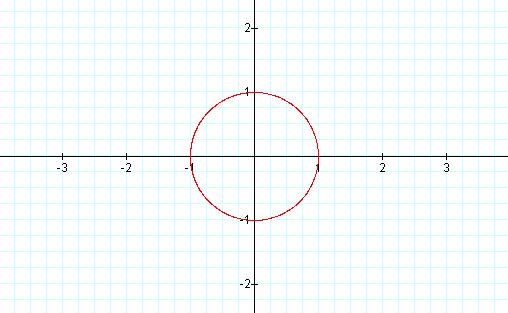
You will
notice that we get a circle with radius one.
Further investigations revealed to me that this will always
be the case††††† when a = b.
† Letís see what
happens when a and b arenít equal.
† Weíll let a
= 2 and vary the values of b.
† What happens when b
= 4?
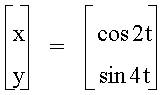
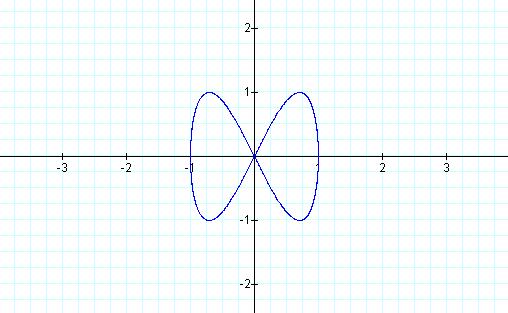
† What happens when b
= 6?
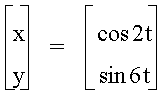
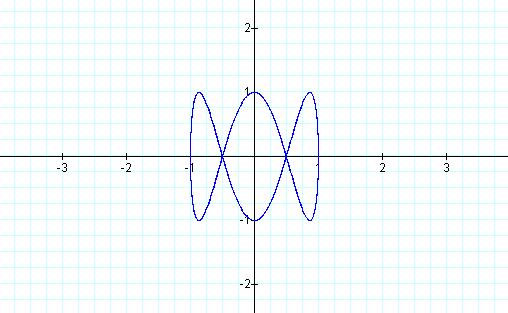
† And when b
= 10 :
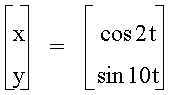
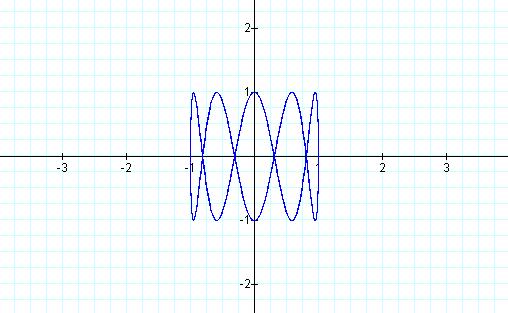
Notice in these examples that the number of circular shapes
created is equal to the value of b divided by the value of a.
† Now letís see what
happens when we hold b constant and vary a.
† Letís make b
= 2.
† Let a = 4
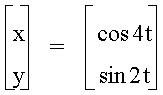
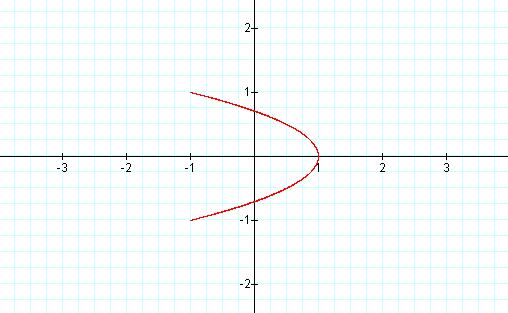
† Let a = 6
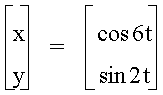
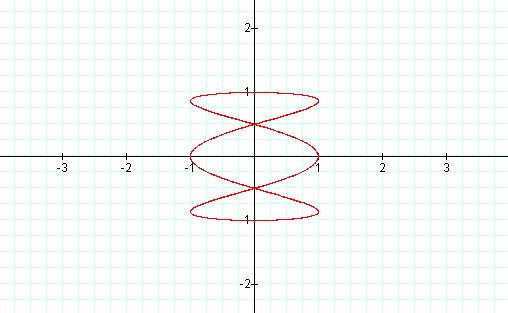
† Let a = 10
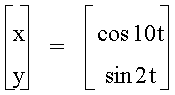
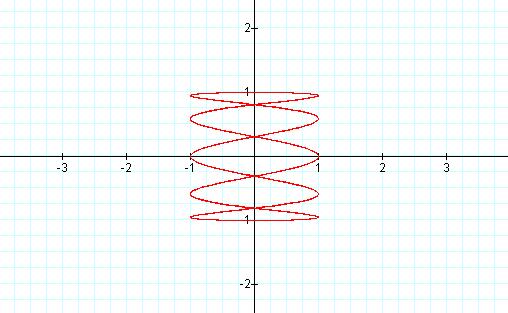
These
values of b seem to produce the same curves for a, except that they are rotated
90 degrees.
________________________________________________________
Just for fun
† Now letís see an
example for large values of a and b.
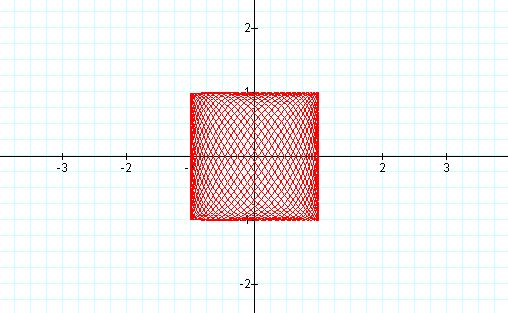
† Here a = 19
and b = 29