
________________________________________________________________________
Polar Equations
By Lauren Lee
________________________________________________________________________
Investigate†† ![]() .
.
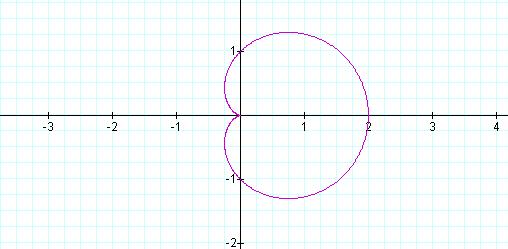
In this
example, a = 1 = b, and k = 1.
When a
and b are equal, we get whatís called an
ďn-leaf
roseĒ.
Letís see
more of these examples.
Let a = 2
= b, and k = 3
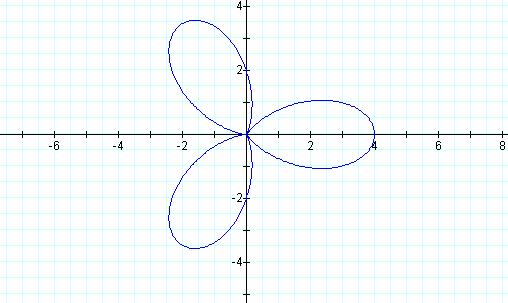
Let a = 2
= b, and k = 4
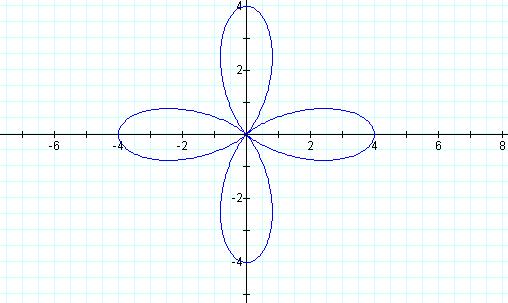
Letís make a prediction about k.† What if a = 2 = b, and k = 9?† My guess is that there will be 9 leaves in the graph.
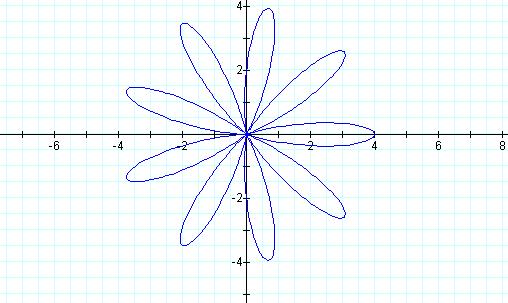
9 leaves!
Letís try one more.† What about when a = 2 = b, and k = 15?
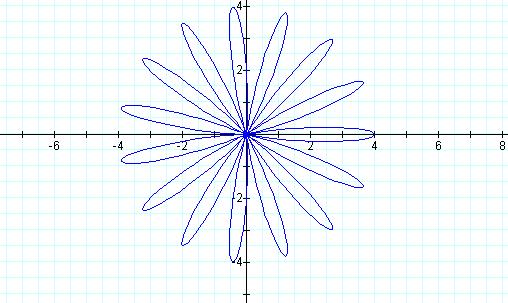
15
leaves!
Now,
letís investigate what happens when a = 0.
![]()
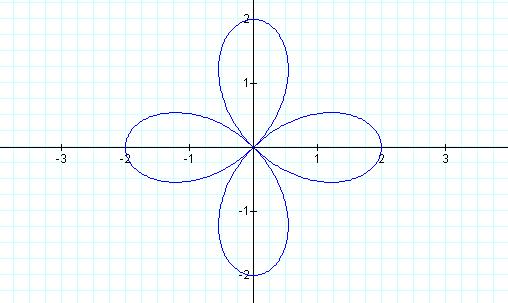
Let b = 2
and k = 2
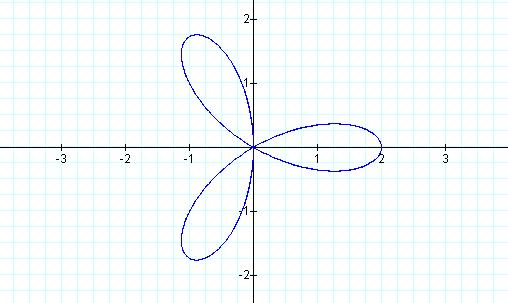
Let b = 2 and k = 3
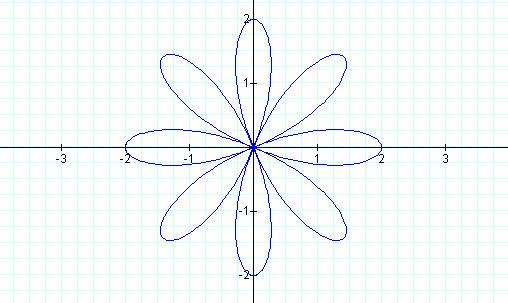
Let b = 2
and k = 4
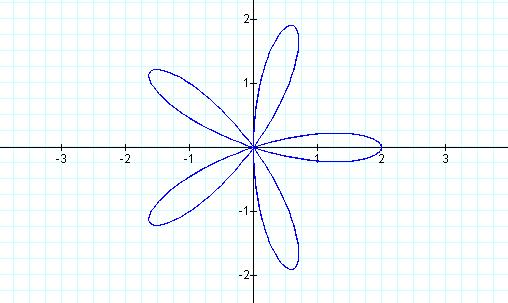
Letís try
one more before making a prediction.
Let b = 2
and k = 5
Do you
see a pattern?† When k is odd, there are
k leaves in the graph.† When k is even,
there are 2k leaves in the graph!
Letís
look at one more.
Let b = 2
and k = 10
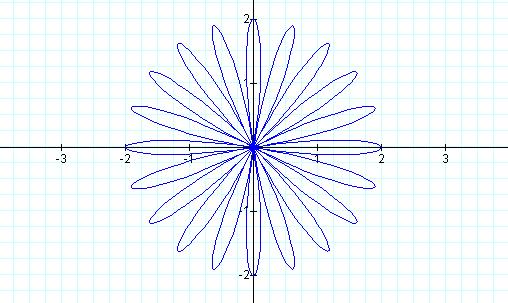
20
leaves!
So letís put this together.† When a equals b, there are k leaves in the graph.† When a is zero and k is odd, there are k leaves in the graph.† When a is zero and k is even, there are 2k leaves in the graph!
Letís do one final investigation.† What if we change cos to sin?
![]()
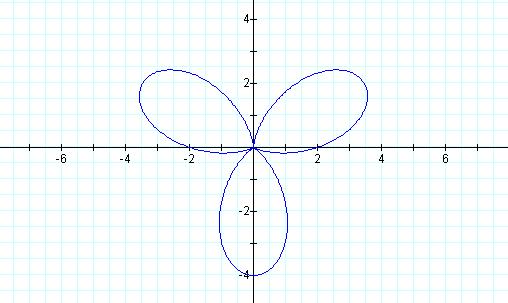
Letís
look at a = 2 = b, and k = 3
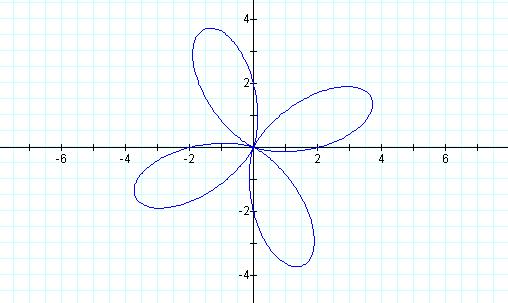
Letís look
at a = 2 = b, and k = 4
Let a = 2
= b, and k = 9
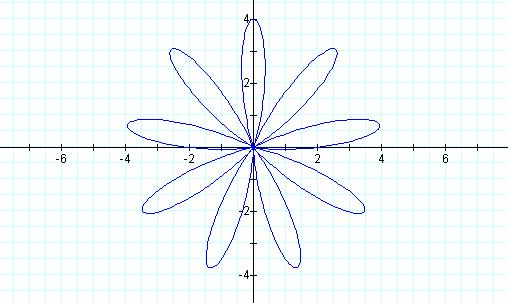
The
graphs of sin are similar to the graphs of cos.† The difference is that the leaves in the sin graphs are shifted
to the right.