
![]()
Exploring parabolas:
y = ax≤ + bx +c
![]()
By:† Lauren Lee
![]()
The
above equation is known as a quadratic equation. A quadratic equation
is an equation that can be expressed in the form of:
![]()
where
a is not equal to zero.
Every
quadratic equation has U-shaped graph called a parabola.
For my first
exploration, I want to start out by looking at a parabola with a fixed a
and b constant.† Let a=1, b=1,
and vary c values.†
Thus our equation is:† y = x≤ + x
+ c.
†Letís look at the graph for values c = -1,
c
= -4, c = 0, c = 1, c = 5.
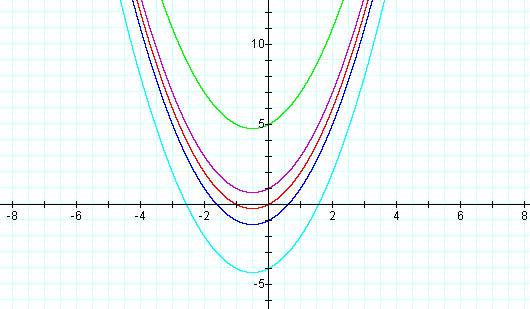
What is seen in our picture is that as the values of c increase, the parabola narrows and the vertex increases.† Similarly, as c decreases, the parabola widens and the vertex decreases.
Now
letís explore what happens when we fix a and c
values.† Let a = 1,
c = 1, and vary b.†
Thus our equation is:† y = x≤ + b
x + 1.
Letís look at the graph for values b = 0, b = -2, b = -4, b = -7, b = 2, b = 4, b = 7.
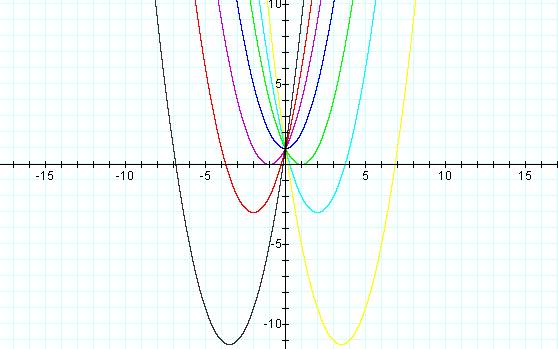
We
can see that the 'highest' parabola is x≤ + 0x + 1,
which also happens to be the upper limit for the parabolas.† As b increases positively, the
parabola dips lower and lower to the left. As b decreases
negatively, it dips lower to the right.†
One more thing to notice is that all of the parabolas contain the point
(0,1).
Finally,
letís explore what happens when we fix b and c.† Let b = 2 and c
= 1 and vary the values for a.†
Thus our equation is:† y = ax≤
+ x + 1.
Letís look at the graph for values a = -1, a = -2, a = -4, a = 0, a = Ĺ, a = 1, a = 2, a = 4.
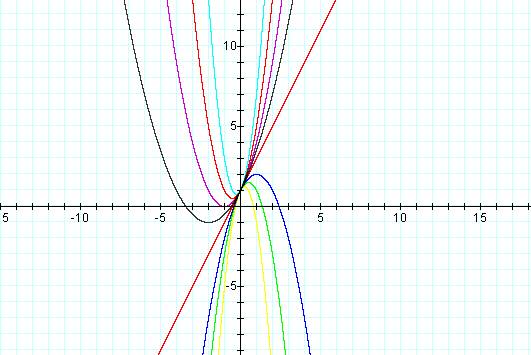
We initially notice that when a is positive, the parabola opens upward (concave up).† Similarly, when a is negative, the parabola opens downward (concave down).† We also see that when a = 0, we are left with the linear equation y = 2x + 1.† Once again, all of the parabolas cross at the point (0,1).†
Finally, we notice that as |a| increases, the parabola narrows, and as |a| decreases, the parabola widens.
Do some more explorations on your own.† How does the shape change?† How does the position change?