Further Explorations with Parabolas
By:† Lauren Lee
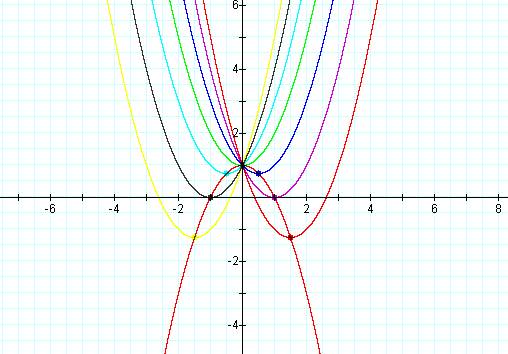
Letís look at y = ax2
+ bx + c again.† Set a = 1 and c = 1 and
vary b.† Letís see what happens when b =
-5, -3, -1, 0, 1, 3, 5.
b = -3, b = -2, b = -1, b = 0, b = 1, b = 2, b = 3
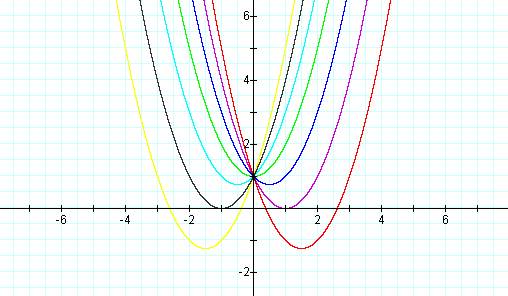
We
can see that all of the parabolas pass through the same point on the y-axis,
(0, 1).† We will also notice for b = 0, the parabola is centered
around the y - axis.† Also we noted
before that as the value of b decreases, the parabola dips further down to the
right.† Similarly, as b increases, the
parabola dips further down to the left.
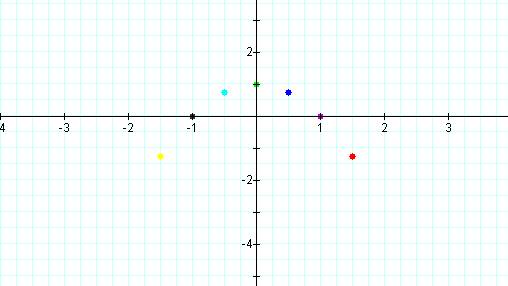
Now letís explore the locus
of the vertices of these parabolas that are graphed.† The vertices are:
(1.5, -1.25) for
b = -3
(1, 0) for b = -2
(0.5, 0.75) for
b = -1
(0, 1) for b = 0
(-0.5, 0.75) for
b = 1
(-1, 0) for b =
2
(-1.5, -1.25)
for b = 3
Letís
plot the vertices and see if we can make any conjectures.
First notice that the vertices appear to form an upside-down parabola.† Also from looking at the vertices, we can see that the roots of this new parabola are x = -1 and x = 1.
Letís try to find the equation of this concave down parabola.
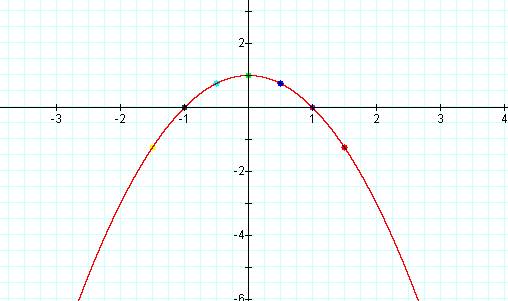
Using our original equation, y = ax2 + bx
+ c, we know that a must be negative since it is
concave down.† So in this case, a
= -1.††† So to solve the equation set y
equal to the roots.
y = (x + 1)(x Ė 1)
By
simplifying we get y = x2 - 1.†
But
since parabola is concave down, the locus of the vertices when a =
1 and c = 1, is the parabola†
y = -x2 + 1.