Exploring Parabolas

By: Lauren Lee

A parabola is the set of points equidistant from a line, called the directrix, and a fixed point, called the focus.

Constructing parabolas:

If you have Geometer's Sketchpad, try to construct your own parabola by following these directions.

First select the “show grid” option. This will help you to place a focus and a directrix for your parabola. Place an arbitrary point on your graph, which will be the focus, and an arbitrary line, which will be the directrix. For my focus, I chose the point (1,2) and for my directrix I chose the x-axis.

Now you will need to construct a point on your directrix. To do this, highlight your directrix, and under “construct” choose the “point on segment” option. Now you have created a “moveable” point on the directrix. Highlight the point and the directrix and construct a perpendicular line. This step is important and you will soon see why!

Our next step is to construct a segment between the focus and our “moveable” point. Then construct the midpoint of the new segment. This ensures that this point on the directrix is equidistant from the focus. So, when we move the point along the directrix, we can see that the midpoint of this segment is always equidistant from our “moveable” point and the focus.

Now, by highlighting the midpoint and the segment, construct a perpendicular line. This line and our other perpendicular line will intersect. The point where they intersect is the point where the focus and directrix are always equidistant! So when we plot a set of these points, we have a parabola!

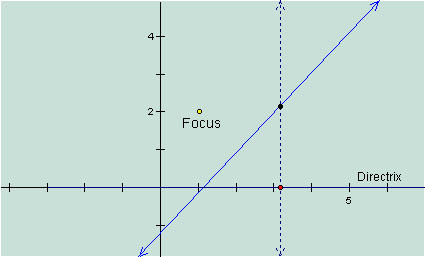
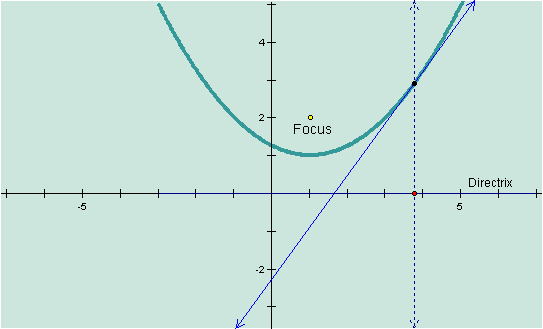
So you might be wondering how this is related to Calculus. You might realize from looking at the picture, that the blue line is the tangent line to the parabola. This allows us to make even more connections involving the first derivative of a function.

Return