EMAT 6690

Heron’s Formula

Ken Montgomery

Although the area formula for a triangle enables one to easily calculate the area of a triangular region, one must be able to measure the height (Equation 1).

Equation 1:

In some cases, as in a farmer’s field for instance, a measure of the height is difficult to obtain, although the individual side lengths are easily measured (Figure 1).

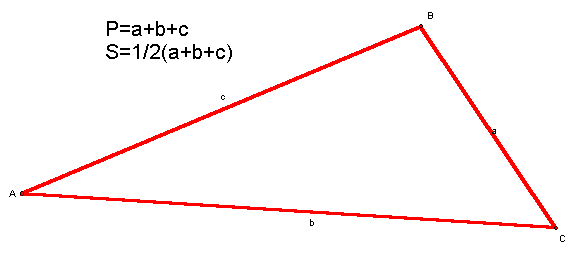
Figure 1: with side lengths, a, b and c

A calculation of area, given the individual side lengths is readily made with use of Heron’s formula (Equation 2), where s, is the semi-perimeter, and is equal to one-half of the Perimeter (Figure 1).

Equation 2:

Equation 3 represents one of the three relations from the Law of Cosines.

Equation 3:

Solving Equation 1 for cos( A), we obtain Equation 4.

Equation 4:

Equation 5 represents a fundamental trigonometric identity:

Equation 5:

Solving Equation 3 for , we obtain Equation 6.

Equation 6:

Substituting from Equation 4, we have Equation 7.

Equation 7: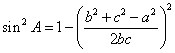

Squaring the term in parenthesis, we obtain Equation 8.

Equation 8:

Rewriting 1 with a common denominator gives Equation 9.

Equation 9:

Distributing the minus sign yields Equation 10.

Equation 10:

Combining like-terms and factoring yields Equation 11.

Equation 11:

Taking the square root of both sides gives Equation 12.

Equation 12:

The area formula for a triangle is given in Equation 13.

Equation 13:

In figure 2, we have , with height h and base, b, partitioned into segments and.

Figure 2: with height, h and partitioned base, b

From Figure 2 and trigonometric ratio of sides, we obtain Equation 14.

Equation 14:

Substitution from Equation 14 into Equation 13 yields Equation 15.

Equation 15:

Substituting from Equation 12, we obtain Equation 16.

Equation 16:

Simplifying yields Equation 17.

Equation 17:

Distributing and rearranging terms yields Equation 18.

Equation 18:

We then write the equivalent relation given in Equation 19.

Equation 19:

Rearranging terms yields Equation 20.

Equation 20:

We rewrite one of the terms in the discriminate to obtain Equation 21.

Equation 21:

We add zero to the discriminate via canceling terms, obtaining Equation 22.

Equation 22:

We then factor the discriminate in Equation 22, yielding the simpler Equation 23.

Equation 23:

We add zero again, via canceling terms, to the two factors of the discriminate obtaining Equation 24.

Equation 24:

These additions of zero allow for the factoring of the discriminate in Equation 24, yielding the more elegant Equation 25.

Equation 25:

Distributing the fraction under the radical, we obtain Equation 26.

Equation 26: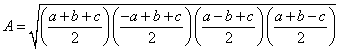

We factor out the one-half from each factor of the radical obtaining Equation 27.

Equation 27: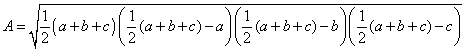

We define semi-perimeter (s) to be half of the perimeter in Equation 28.

Equation 28:

Substitution from Equation 28 allows for the familiar expression of Heron’s formula in Equation 29.

Equation 29:

Click here to open HeronsFormula.gsp and explore the relationship between perimeter and area.

Return to EMAT 6690