EMAT 6690

Ken Montgomery

Brahmagupta’s Formula

Given Quadrilateral ABCD, draw diagonal(Figure 1) dividing the quadrilateral into the two triangles,and.

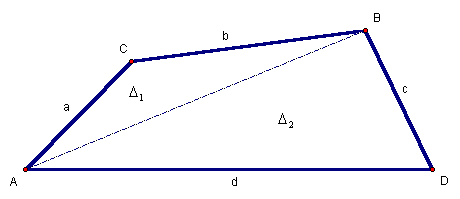
Figure 1: Quadrilateral ABCD

Let the areas of andbe given byand, respectively. Then the total area of the quadrilateral () is given in Equation 1.

Equation 1:

Applying trigonometry toand, respectively, we obtain the relationships given in Equations 2 and 3.

Equation 2:

Equation 3:

Substitution of Equations 2 and 3 into Equation 1, yields Equation 4.

Equation 4:

We, then square both sides in Equation 5.

Equation 5:

Squaring the binomial term on the right side yields Equation 6.

Equation 6:

Factoring out gives Equation 7.

Equation 7:

From the Law of Cosines, we obtain Equations 8 and 9.

Equation 8:

Equation 9:

Setting Equations 8 and 9 equal, via the transitive property yields Equation 10.

Equation 10:

Rearranging Equation 10, we obtain Equation 11.

Equation 11:

We then square both sides of Equation 11.

Equation 12:

Squaring the binomial term on the left yields Equation 13.

Equation 13:

Next, we multiply both sides by c to obtain Equation 14.

Equation 14:

Distributing on the left hand side gives Equation 15.

Equation 15:

Factoringout of the left side results in Equation 16.

Equation 16:

Rearranging Equation 16, we have Equation 17.

Equation 17:

We restate Equation 7, here as Equation 18.

Equation 18:

Adding zero to both sides, we have Equation 19.

Equation 19: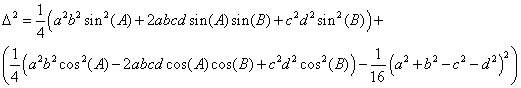

Factoring, we have Equation 19, we obtain Equation 20.

Equation 20: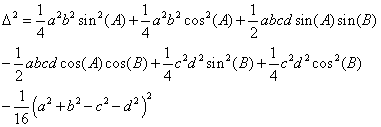

Factoring, again, we have Equation 21.

Equation 21: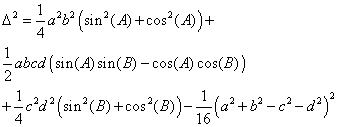

Simplifying, via a trigonometric identity (), we have Equation 22.

Equation 22:

We make use of another trigonometric identity, given in Equation 23.

Equation 23:

Applying Equation 23 to Equation 22, we obtain Equation 24.

Equation 24:

Rearranging and factoring, we obtain Equation 25

Equation 25: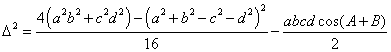

We next multiply out the term, in Equation 26.

Equation 26:

Distributing and simplifying, we have Equation 27.

Equation 27:

Substitution into Equation 25, yields Equation 28.

Equation 28:

Distributing the 4 gives Equation 29.

Equation 29:

Simplifying, we have Equation 30.

Equation 30:

To factor the left side, we add and subtract , obtaining Equation 31.

Equation 31:

Working with the numerator of the first fraction, we rearrange terms, applying the commutative property of addition, to obtain Equation 32.

Equation 32:

Rewriting the terms,and, we have Equation 34.

Equation 34:

Rewriting , we obtain Equation 35.

Equation 35:

Adding zero, via canceling terms, we rewrite Equation 35 equivalently in Equation 36.

Equation 36: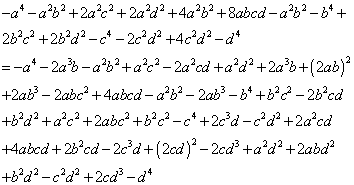

Equation 36, then factors into the two products presented in Equation 37.

Equation 37: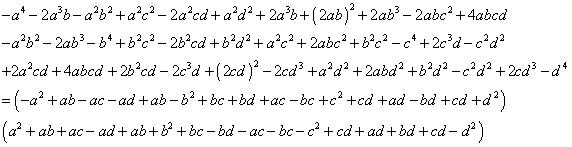

The right-hand side of Equation 38, will then factor into the four products of Equation 38.

Equation 38: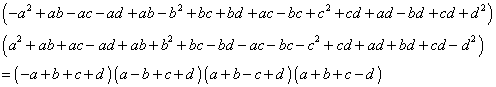

Substituting from Equation 38, into Equation 31, we obtain Equation 39.

Equation 39:

Writing 16 as its prime factorization, we obtain Equation 40.

Equation 40:

Rewriting –a as a – 2a, -b as b – 2b, -c as c – 2c and –d as d – 2d, yields Equation 41.

Equation 41:

Dividing the right-most term in each of the four factors by 2, results in Equation 42.

Equation 42:

We define semi-perimeter in Equation 43.

Equation 43:

Substituting from the relation in Equation 43, into Equation 42, we obtain Equation 44.

Equation 44:

Factoring out abcd in the second fraction, we obtain Equation 45.

Equation 45:

Applying the Cosine half-angle trigonometric identity, results in Equation 46.

Equation 46:

Taking the square root of both sides, we obtain the generalized formula of Brahmagupta, which does not require that the quadrilateral be circumscribed. This result is also known as Bretschnieder’s formula (Equation 47).

Equation 47: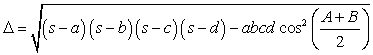

Open BrahmaguptasFormula.gsp compare the calculated measurements of area.

Return to EMAT 6690