
EMAT
6690
Ken
Montgomery
The
Three Tangent Circles Problem
Problem Statement: Given two line segments, construct externally tangent circles with these segments and construct a common external tangent line. Then construct a circle tangent to the two given circles having the same external tangent line. Find the radius, c, of the new circle in terms of the radii a, and b, of the first two circles.
Part 1: Construction of externally tangent circles and tangent line
We
begin with
arbitrary line segments a, and b and construct the
green circle
with center B and radius, b. We construct ![]() and then we construct
the red, dashed circle, with center C, but with radius, a.
Notice
that the intersection of Circle C and
and then we construct
the red, dashed circle, with center C, but with radius, a.
Notice
that the intersection of Circle C and![]() is A, where we construct the red circle A,
which is tangent to circle B (Figure 1).
is A, where we construct the red circle A,
which is tangent to circle B (Figure 1).
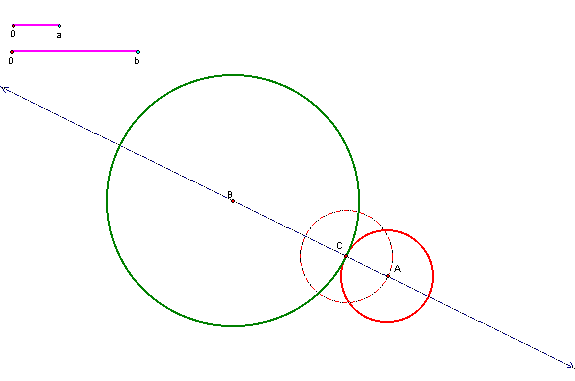
Figure 1: Arbitrary line segments, a and b, with tangent circles A and B
If
we consider the
segment, ![]() to
be the hypotenuse of a right triangle, then the length of
the base would correspond to the horizontal distance between A
and B.
The problem now becomes the construction of the vertex F,
corresponding
to the right angle of
to
be the hypotenuse of a right triangle, then the length of
the base would correspond to the horizontal distance between A
and B.
The problem now becomes the construction of the vertex F,
corresponding
to the right angle of ![]() .
We know that the height of the triangle should be equal to b
– a, and that the length of the hypotenuse is equal to b + a.
Assume
.
We know that the height of the triangle should be equal to b
– a, and that the length of the hypotenuse is equal to b + a.
Assume ![]() and
and![]() ,
then
,
then ![]() represents the base
of the triangle and we have Equation 1 from the Pythagorean theorem.
represents the base
of the triangle and we have Equation 1 from the Pythagorean theorem.
Equation
1: ![]()
Solving Equation 1 for![]() yields
Equation 2.
yields
Equation 2.
Equation
2: ![]()
Multiplying out the squared terms yields Equation 3.
Equation
3: ![]()
Distributing the minus sign gives Equation 4.
Equation
4: ![]()
Combining like terms provides Equation 5.
Equation
5: ![]()
Taking the square root of both sides gives Equation 6.
Equation
6: ![]()
Simplification yields Equation 7, which gives the horizontal distance in terms of a and b, between Circles A and B.
Equation
7: ![]()
To construct the result
of Equation
7, we first find the midpoint of![]() and
construct a circle, with this segment as its diameter. A
line, perpendicular to
and
construct a circle, with this segment as its diameter. A
line, perpendicular to![]() and
its intersections with the circle are then constructed.
By similar triangles, the orange segment,
and
its intersections with the circle are then constructed.
By similar triangles, the orange segment,![]() is
a construction of the desired length,
is
a construction of the desired length, ![]() (Figure
2).
(Figure
2).
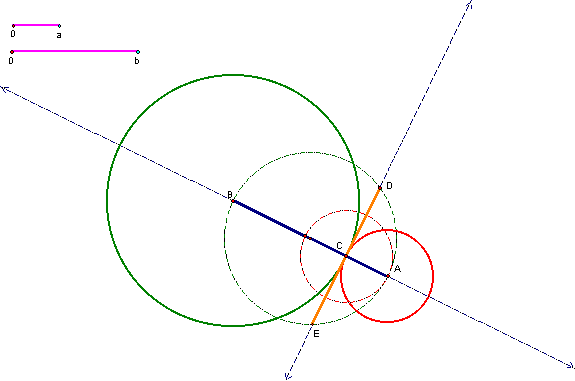
Figure
2: Construction of ![]() ,
given by the orange segment,
,
given by the orange segment, ![]()
Since
the base of![]() corresponds
to segment
corresponds
to segment![]() and
the height of the triangle should have the value b
– a, we construct a circle, with center A and radius
congruent to
and
the height of the triangle should have the value b
– a, we construct a circle, with center A and radius
congruent to![]() .
We also construct a circle, centered at B, but with
radius b – a. The intersection, F, of these two circles
is the
third vertex of our right triangle (Figure 3).
.
We also construct a circle, centered at B, but with
radius b – a. The intersection, F, of these two circles
is the
third vertex of our right triangle (Figure 3).
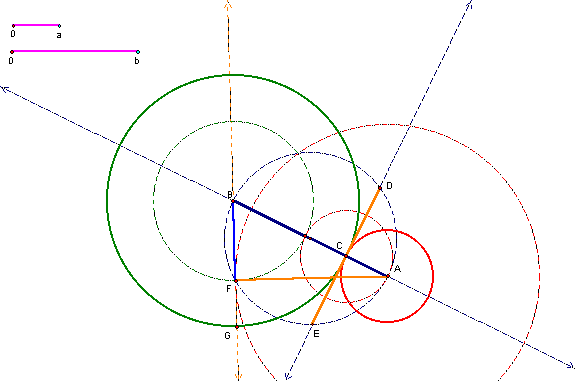
Figure
3: Construction of ![]()
At
this point, we wish to construct a line, tangent to Circles A
and B.
Since we know that the line will be tangent to each circle and also a
distance,
a (the radius of Circle A), from the respective
vertices, A
and B, we know that the line will be parallel to![]() .
To simplify figure four, we hide part of our previous
construction and proceed to construct a line, parallel to
.
To simplify figure four, we hide part of our previous
construction and proceed to construct a line, parallel to![]() ,
through point G (Figure 4).
,
through point G (Figure 4).
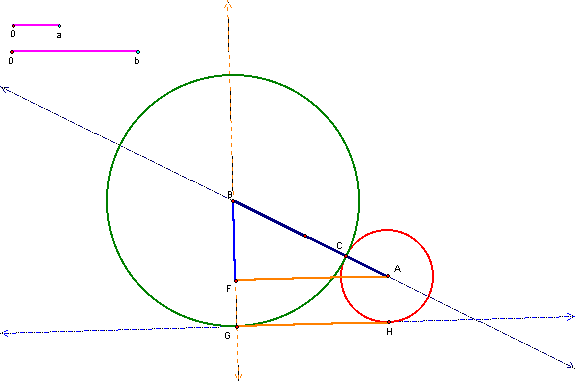
Figure
4: ![]() is
tangent to
is
tangent to ![]() and
and![]()
Part 2: Derivations
of radius, c
and distance,![]() as a function of radii a, and b
as a function of radii a, and b
We
will next wish
to construct a third circle, externally tangent to![]() and
and![]() and
tangent to
and
tangent to![]() .
If we now consider the segment,
.
If we now consider the segment, ![]() to
be the hypotenuse of a right triangle, then the length of
the base would correspond to the horizontal distance between B
and C.
We know that the height of the triangle should be equal to b – c,
and that the length of the hypotenuse is equal to b + c. Assume
to
be the hypotenuse of a right triangle, then the length of
the base would correspond to the horizontal distance between B
and C.
We know that the height of the triangle should be equal to b – c,
and that the length of the hypotenuse is equal to b + c. Assume
![]() and
and![]() ,
then
,
then ![]() represents
the base of the triangle and from the Pythagorean
theorem we have Equation 8.
represents
the base of the triangle and from the Pythagorean
theorem we have Equation 8.
Equation
8:![]()
Solving Equation 8 for![]() ,
we have Equation 9.
,
we have Equation 9.
Equation
9:![]()
Squaring the binomial terms yields Equation 10.
Equation
10:![]()
Simplifying Equation 10, provides Equation 11.
Equation
11:![]()
Taking the square root of both sides, gives Equation 12.
Equation
12:![]()
Simplification allows us to obtain Equation 13.
Equation
13:![]()
We have an expression representing the horizontal (x-axis) distance between B and C, but it is in terms of the radius, c, which we still do not know and now seek to determine. Again, using the Pythagorean theorem, we obtain Equation 14.
Equation
14:![]()
Solving Equation 14 for![]() ,
we obtain Equation 15.
,
we obtain Equation 15.
Equation
15:![]()
Squaring the binomial terms yields Equation 16.
Equation
16:![]()
Distributing the minus sign and simplifying gives Equation 17.
Equation
17:![]()
Taking the square root of both sides, gives Equation 18.
Equation
18:![]()
Further simplifying and
solving
Equation 18 for![]() yields Equation 19.
yields Equation 19.
Equation
19:![]()
We restate a previous results: Equation 7 here as Equation 20 and Equation 13 as Equation 21.
Equation
20:![]()
Equation
21:![]()
Substitution of Equations 20 and 21 into Equation 19 results in Equation 22.
Equation
22:![]()
Division of both sides by 2 yields Equation 23.
Equation
23:![]()
Rewriting the left side of the equation, we have Equation 24.
Equation
24:![]()
Factoring the left side, we obtain Equation 25.
Equation
25:![]()
Solving Equation 25 for![]() ,
provides Equation 26.
,
provides Equation 26.
Equation
26: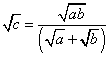
Taking the square root of both sides, we have Equation 27.
Equation
27: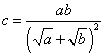
Substitution of this
result into
Equation 13 yields the expression for![]() ,
in Equation 28, below.
,
in Equation 28, below.
Equation
28: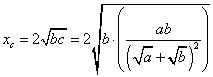
Simplifying this equation yields Equation 29.
Equation
29: ![]()
Now that we have
obtained
expressions, in terms of a and b, for ![]() (the horizontal
distance between B and C), and c, the radius of
(the horizontal
distance between B and C), and c, the radius of
![]() ,
we return to our problem of constructing a third circle,
,
we return to our problem of constructing a third circle, ![]() tangent
to
tangent
to![]() and
externally tangent to
and
externally tangent to![]() and
and
![]() .
.
Part 3: Construction of a third circle
externally
tangent to circles A, B, and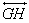
In our construction, we will make use of the relations provided in Equation 13 and Equation 27. Since Equation 13 depends upon the value of c, we begin with a construction of this value. Equation 27 is restated below as Equation 30.
Equation
30: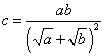
Squaring the binomial in the denominator and applying the commutative property of addition, we obtain Equation 31.
Equation
31:![]()
Dividing both sides of the equation by a, yields the ratio given in Equation 32.
Equation
32:![]()
Each of the terms in
this ratio is
easily constructible, via similar triangles. First, we construct![]() ,
with radius a + b. Then we construct
,
with radius a + b. Then we construct![]() ,
with length,
,
with length, ![]() (Figure 5).
(Figure 5).
Figure
5: Construction of![]()
We next hide![]() and
construct
and
construct![]() ,
with radius
,
with radius![]() .
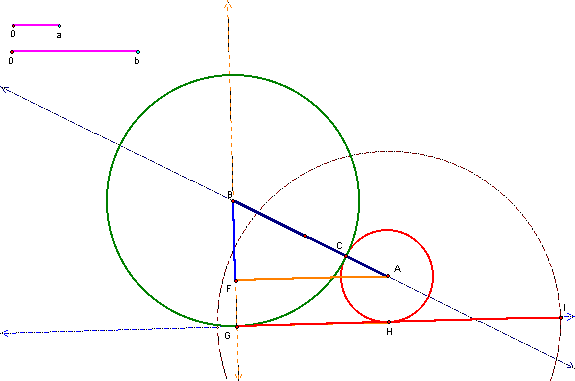
We wish to construct an isosceles triangle, with base, b.
So we next construct
.
We wish to construct an isosceles triangle, with base, b.
So we next construct![]() ,
with radius, b. We then construct the intersection
of
,
with radius, b. We then construct the intersection
of![]() and
and![]() at
J (Figure 6).
at
J (Figure 6).
Figure
6: Construction of![]()
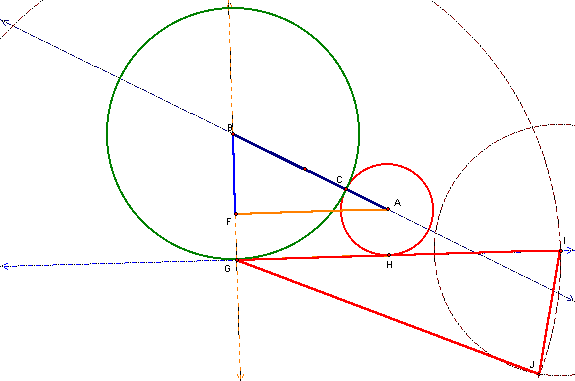
We next hide![]() and
and![]() and
construct another circle with center, G and
radius, a. We construct and connect the intersections of this
circle and
sides
and
construct another circle with center, G and
radius, a. We construct and connect the intersections of this
circle and
sides![]() and
and![]() ,
to obtain
,
to obtain![]() ,
which, by Equation 32 and similar triangles, has length, c
(Figure 7).
,
which, by Equation 32 and similar triangles, has length, c
(Figure 7).
Figure
7: Construction of![]() ,
with length equal to c
,
with length equal to c
We next make use of Equation 13, restated below in Equation 33.
Equation
33: ![]()
This is a relatively
simple
construction that we have already done for ![]() ,
previously. We construct a right triangle, inscribed in
a circle, with hypotenuse equal to b + c. Since the height of
the right
triangle (with the hypotenuse as the base) is equal to
,
previously. We construct a right triangle, inscribed in
a circle, with hypotenuse equal to b + c. Since the height of
the right
triangle (with the hypotenuse as the base) is equal to![]() ,
by similar, right triangles, we construct the
intersections of the circle and the line perpendicular at the point
joining the
lengths, b and c (Figure 8).
,
by similar, right triangles, we construct the
intersections of the circle and the line perpendicular at the point
joining the
lengths, b and c (Figure 8).
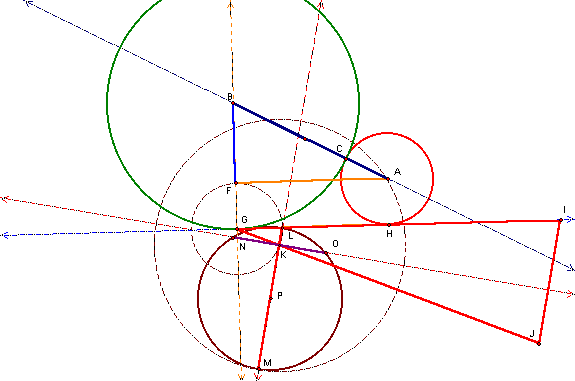
Figure
8: Construction of![]()
In Figure 8, we have
constructed
the circle with center, K and radius, b. We then
constructed ![]() and
and![]() ,
which has length, b + c. We then construct the
midpoint, P, of
,
which has length, b + c. We then construct the
midpoint, P, of ![]() and
and![]() .
A line, perpendicular to
.
A line, perpendicular to![]() is
constructed at K, the point separating the segments
equal to b and c, respectively. Then, we construct
is
constructed at K, the point separating the segments
equal to b and c, respectively. Then, we construct![]() ,
which has length equal to
,
which has length equal to ![]() .
Next, we hide some of this construction and construct a
circle, with center, G and radius
.
Next, we hide some of this construction and construct a
circle, with center, G and radius![]() (Figure
9).
(Figure
9).

Figure
9: Construction of![]() ,
with radius equal to
,
with radius equal to![]()
In Figure 9, we also
constructed a
line, perpendicular to![]() at
Q. We next (Figure 10), construct a circle, with
center, Q and radius equal to c (congruent to
at
Q. We next (Figure 10), construct a circle, with
center, Q and radius equal to c (congruent to![]() )
and its intersection (R) with the perpendicular
line.
)
and its intersection (R) with the perpendicular
line.
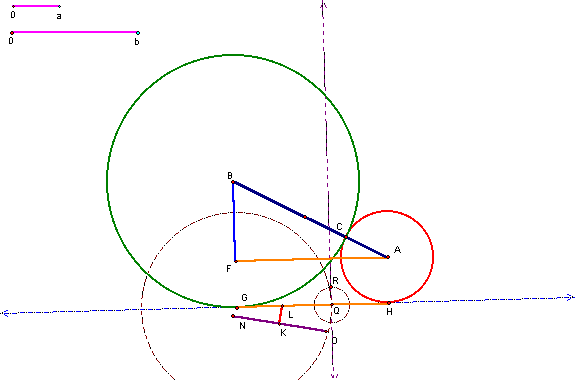
Figure
10: Construction of![]() ,
with radius, c
,
with radius, c
At this stage, we hide
unnecessary
parts of the construction and construct the third, externally tangent
circle (![]() ),
with radius, c, which is a horizontal distance,
),
with radius, c, which is a horizontal distance,![]() from
the point, B (Figure 11).
from
the point, B (Figure 11).
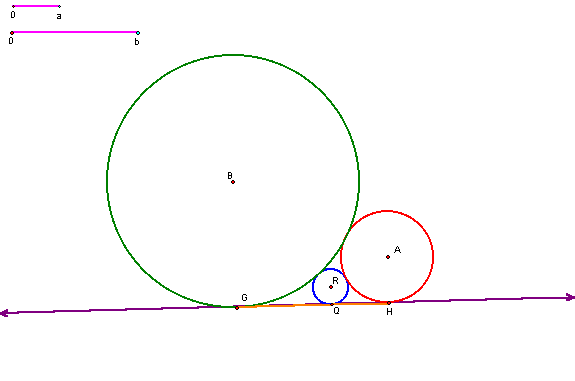
Figure 10: Construction of three, externally tangent circles and a mutually tangent line
Open the file, ThreeTangentCircles.gsp to explore this construction and verify that it is valid for different values of a, and b.
Alternate statement
of Equation
27
Although our derivation of formulas culminated in Equations 27 and 29 (below), Equation 27 is rewritten, in a more aesthetic form.
Equation
27: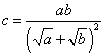
Equation
29: ![]()
We begin with Equation 27, given here as Equation 34.
Equation
34: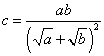
Solving Equation 34 for
![]() ,
we have Equation 35.
,
we have Equation 35.
Equation
35:![]()
Squaring the binomial term yields Equation 36.
Equation
36:![]()
Applying the distributive property, we obtain Equation 37.
Equation
37:![]()
Factoring the right side, we have Equation 38.
Equation
38:![]()
Taking the square root of both sides yields Equation 39.
Equation
39:![]()
We next divide both
sides of the
equation by![]() (Equation
40).
(Equation
40).
Equation
40:![]()
This division results in Equation 41.
Equation
41:![]()
Applying the commutative property of addition to the right side, we obtain Equation 42.
Equation
42:![]()
Derived results are summarized below.
![]()
and
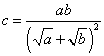 or
or ![]()