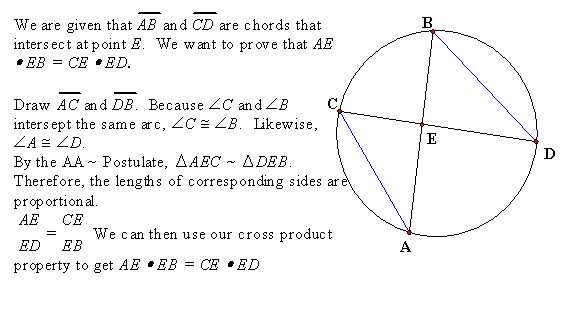
Day 8 – Lengths of Segments of
Chords
When
two chords intersect in the interior of a circle, each chord is divided into
two segments which are called segments of
a chord. The following theorem gives
a relationship between the lengths of the four segments that are formed.
There
is a special relationship for the measures of the segments formed by
intersecting chords. This relationship
is stated in the following theorem:
THEOREM:

If two chords intersect in the
interior of a circle,
then the product of the lengths of
the segments of
one chord is equal to the product
of the lengths of the
segments of the other chord.
Proof: