
Medians of a Triangle
By: Ginger Rhodes
Problem: Prove that the
three medians of a triangle are concurrent and that the point of concurrence,
the centroid, is two-thirds the distance from each vertex to the opposite side.
For the definition of a
median of a triangle click HERE.
Let us begin by
constructing two medians of a given triangle. Let the point of intersection of
the medians be labeled point G.
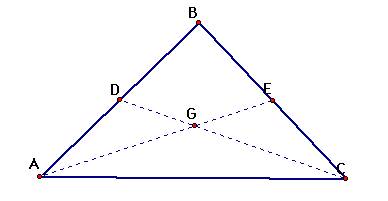
So BD = DA and BE = EC.
Now, I will construct a
line through B and G that intersects segment AC.
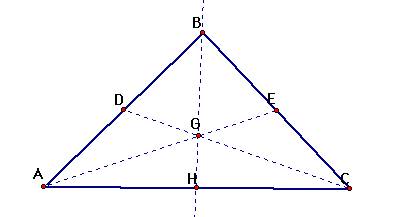
Since D is the midpoint of
segment BA and E is the midpoint of BC I can let BD = AD and BE = EC. Using
Cevaís Theorem (proved in final assignment, click HERE to take a look),
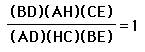
By substitution,
![]()
Therefore,
![]()
This implies AH = HC and BH is a median. Since BH was
constructed to go through G, I can now say the three medians are concurrent.
Now
to letís show the centroid is two-thirds the distance from each vertex to the opposite
side.
We can use
∆DEG~∆CAG by AA~. [DE is parallel to AC because D and E are the
midpoints of the sides of the triangle, which implies alternate interior angles
are congruent]
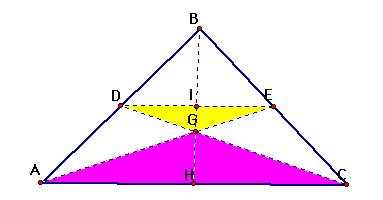
Since D and E are
midpoints of segments BA and BC, respectively, and therefore I can conclude
DE=1/2AC. Now, triangle DIG and triangle CGH are similar by
Angle-Angle-Similarity, by a ratio 1:2. Using this, I can say IG=1/2GH.
I showed BH is the median
of ∆ABC and H is the midpoint of AC earlier; therefore GH and GI are the
medians of ∆AGC and ∆DEG, respectively.
Since I is on segment DE
and the endpoints of segment DE are the midpoints of the sides of the triangle
we can conclude BI = IH.
Now, by segment addition
postulate we know BI+IG+GH=BH
BIĖIG+IG+IG+GH =BH, add
and subtract IG from the same side of the equation
GH+2IG+GH=BH, since
IG+GH=IH and IH=BI
GH+GH+GH=BH, since
IG=1/2GH or 2IG=GH
GH=1/3BH
So, letís use segment
addition postulate again to get BG+GH=BH.
Now we can make a substitution
to get BG+1/3BH=BH.
Subtract 1/3BH from both
sides to get BG=2/3BH.
This shows the centroid,
point G, is two-thirds the distance from the vertex B to the opposite side AC.
We can use a similar proof to show the other two vertices.