
More on Parabolas
By: Ginger Rhodes
Look at y = x 2 + bx + 1 for
different values of b. What do you notice about the “movement” of
the parabola as b is changed? Click HERE
for an animation.
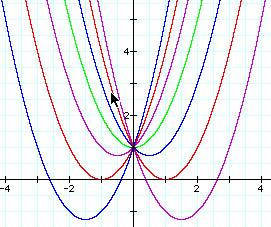
Notice the y-intercept is the same point
(0, 1) for each graph, which makes sense because if you substitute zero in for
x you will always have the + 1 to get an y-coordinate of 1.
At a closer look there are two roots when 2
< b and b < -2,
one root when b = 2 and b = -2, and no
roots when -2 < b < 2.
Now, what does the graph of the locus of
the
vertices of the set of parabolas graphed
when b varies in y = x 2 + bx + 1 look like?
Remember, the vertex can be found using the
line of symmetry x = -b / 2a.
First, find –b / 2a (the x-coordinate
of the vertex)
and then substitute in for x to find the
y-coordinate.
Since a = 1 we can use –b/2.
I will substitute x = -b / 2 into the
following equation
y = x 2 + bx + 1
y = (-b/2)2 + b(-b/2) + 1
So, y = -b2 / 4 + 1
Therefore, the vertices include
(-1.5, -1.25), (-1,0), (-.5, .75), (0,1),
(.5, .75), (1,0), and (1.5,1.25).
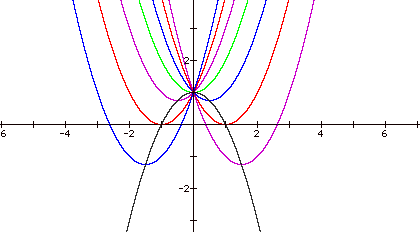
It appears to be a parabola!
How can we find the equation of the
parabola?
We know x = -b/2 and y = -b2 / 4
+ 1,
so let’s solve for b and set the two
equations equal to each other.
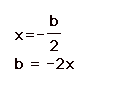
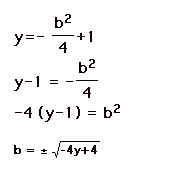
Therefore,
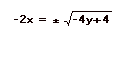
and
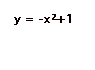
What happens as c changes? Click HERE to explore.
What happens as a changes? Click HERE to explore.
Let’s take a different look at the
equation 0 = x 2 + bx + 1.
What does it look like in the xb plane?
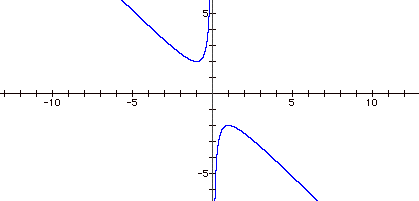
Now, suppose we take b = 3, and overlay
this equation on the graph. Notice we add a line parallel to the x-axis. Where
the horizontal line b = 3 intersects the graph is the roots for the original
equation.
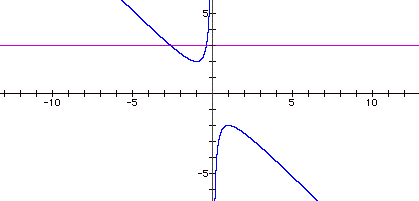
Notice, at a closer look there are two
roots when 2 < b and b < -2,
one root when b = 2 and b = -2, and no
roots when -2 < b < 2 (just as before!!)
What happens when c = -1?
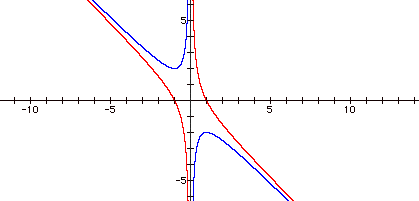
Other c values?
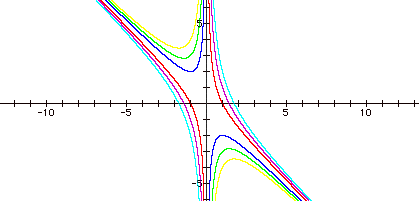
c = -3, -2, -1, 1, 2, and 3
What about c = 0?
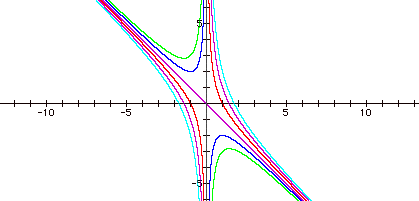
What relationship does 2x + b = 0 have with
the other graphs?
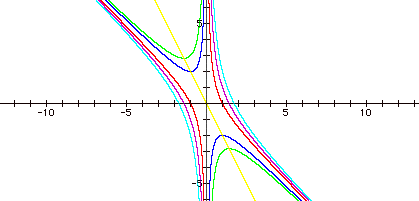
It appears to go through the vertex.
Thinking back to before we know this point
is a single root and where the quadratic is tangent to the x-axis.
This point is also the vertex.
Before we discussed x = -b / 2a is the
x-coordinate of the vertex.
Solve for b and substitute a = 1 you get b
= -2x.