Assignment 1
Write up
Two Linear Functions
Let f(x) = nx + .5
where n ![]() R and n>0.
R and n>0.
Let g(x) = -nx + .5
where n ![]() R and n>0.
R and n>0.
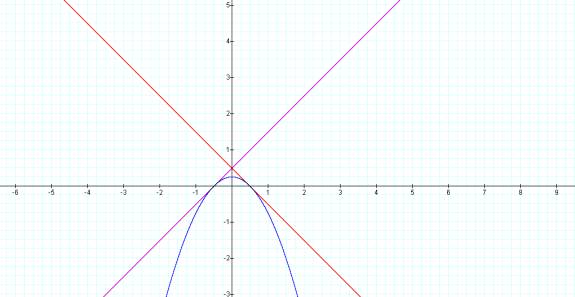
g(x)=-nx+.5 F(x)=nx+.5
![]()
Then let h(x) = f(x)g(x)
h(x) = (nx +.5)(-nx + .5)
![]()
To show the point of tangency we must show the point where:
A. ![]()
