Altitudes of a Triangle
EMAT 6680
![]()
Investigation: Construct the three altitudes of a triangle and prove that they are concurrent.
We will begin our investigation by looking at several triangles and their
altitudes.
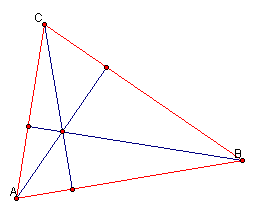
Here we see an acute
triangle. It appears that all three of the altitudes intersect in a single
point.
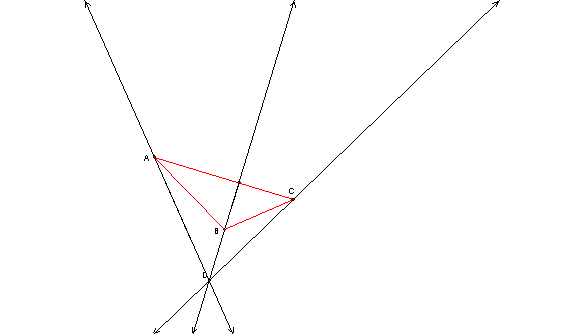
Necessary definitions
and theorems
Definition of concurrent:
A number of lines are concurrent if they have exactly one point in common.
Definition of altitude of a triangle:
A line segment drawn from a vertex of the triangle
perpendicularly to the side opposite the vertex.
Definition of orthocenter:
The point of concurrence for the three altitudes
of a triangle.
Theorem of perpendicular bisectors:
The three perpendicular bisectors of the sides of
a triangle are concurrent.
![]()
Outline of proof:
Proof:
![]() By definition of an altitude of a triangle,
By definition of an altitude of a triangle, ![]() is perpendicular to
is perpendicular to ![]() ,
,![]()
![]() and
and ![]()
![]() .
.
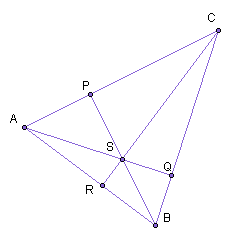
![]()
![]() and passing through point A.
and passing through point A.
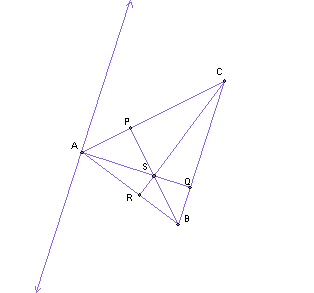
Similarly, construct ![]()
![]() and passing through point C and
and passing through point C and ![]()
![]() and passing through point B.
and passing through point B.
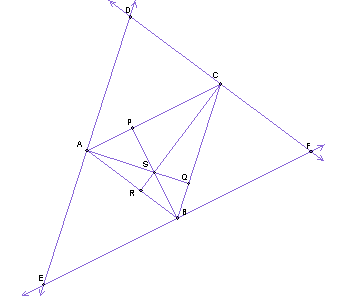
Since ![]()
![]() and
and ![]() is a transversal through these segments, angle
is a transversal through these segments, angle ![]()
![]() by definition of perpendicular lines.
by definition of perpendicular lines.
![]()
![]() and
and ![]()
![]() .
.
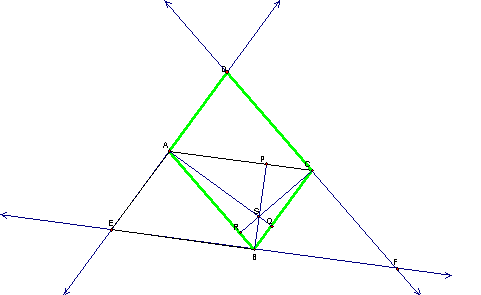
![]()
![]() and
and ![]()
![]() . By definition of a parallelogram, ABCD forms a parallelogram and thus
AD=BC.
. By definition of a parallelogram, ABCD forms a parallelogram and thus
AD=BC.
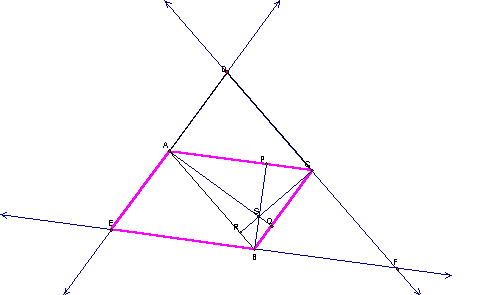
![]()
![]() and
and ![]()
![]() .By definition of a parallelogram, ACBE forms a parallelogram and thus EA=BC.
.By definition of a parallelogram, ACBE forms a parallelogram and thus EA=BC.
![]() and separates the segment
and separates the segment ![]() into two congruent parts
into two congruent parts ![]() and
and ![]() . Thus,
. Thus, ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() .
.
![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() and that
and that ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() . Since we have shown that each segment
. Since we have shown that each segment ![]() ,
,![]() and
and ![]() is a perpendicular bisector then all three segments must be concurrent by
the theorem for the concurrence of the perpendicular bisectors of a triangle.
is a perpendicular bisector then all three segments must be concurrent by
the theorem for the concurrence of the perpendicular bisectors of a triangle.
Return to Janet Shiver's Home Page