Similar Triangles Everywhere
By Janet M. Shiver
EMAT 6680
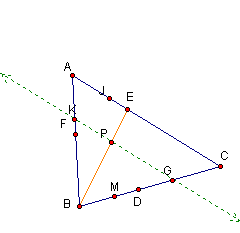
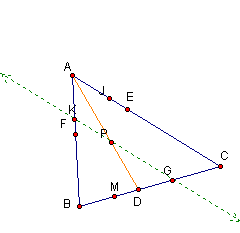
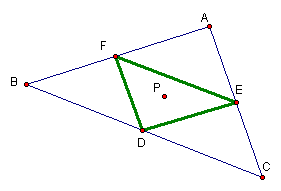
We will begin our investigation by considering an arbitrary triangle ABC and a point P inside the triangle. We will draw line segments from each of the vertices through point P until they intersect with the opposite side.
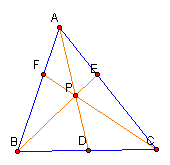
Next we will look at the product of segments AF, BD and EC in comparison to the product of the segments FB, DC and EA. Click Here to explore for yourself. Manipulate each of the vertices while keeping an eye on the product of each. Here is an example of what you might find below.
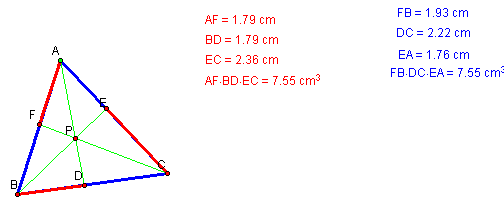
After moving each of the vertices several times, it is apparent that the products will always remain equal as long as point P remains inside the triangle and points A, B and C remain distinct from points D, E and F.
It will also be helpful to us at this point to look at the ratio of the products of the segments.
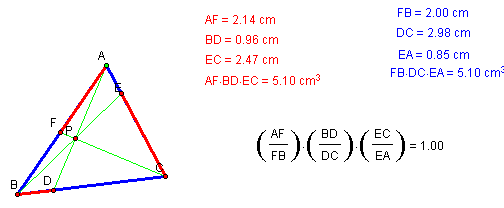
It appears that the product of the ratios of the listed segments is always one.
Conjecture:
Given any triangle
ABC and a point P in the interior with three segments AD, FC and BE all passing
through p, then 
.
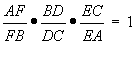Proof:
Given triangle ABC
with point P in its interior and three segments AD, FC and BE all passing
through point P.
PART 1
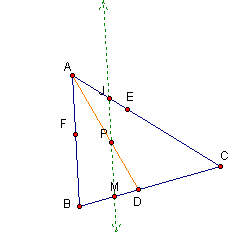
1A. Construct a line parallel to AB and passing through point P.
To help visualize
the next part of the proof I have hidden the segments AD and BE.
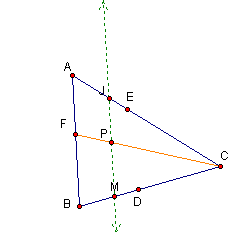
by corresponding angles.
By angle-angle similarity,
triangle AFC is similar to triangle JPC. Thus, 
.
by corresponding angles.
By angle-angle similarity,
triangle BFC is similar to triangle MCP. Thus, 
.
By substitution,
.
Cross multiplying
we get (AF)(MP) =(BF)(JP).
Dividing, we see that
1B. Now, I will redraw
segment BE while hiding segments FC and AD.
by
the reflexive property.
by
corresponding angles.
By angle-angle similarity, triangle ABE is similar
to triangle JPE.
Thus, 
.
1C. Now I will redraw segment AD while hiding
segments FC and BE.
by
the reflexive property.
by
corresponding angles.
By angle-angle similarity, triangle ADB is similar
to triangle PDM.
Thus, 
.
Since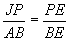 
and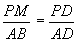 
,
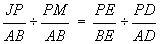
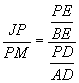
Using substitution (1A),
.
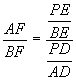PART 2
1A. Construct a line parallel to AC and passing through point P.
Using an argument
similar to 1A, we can show that triangle CBE is similar to triangle GBP.
Thus, 
.
Again using argument
1A we see that triangle ABE is similar to triangle KBP. Thus, 
.
By substitution,
.
By multiplying, we
see that 
.
1B. Now I will redraw
segment AD while hiding segments FC and BE.
Using an argument similar to 1B. We can show that
triangle ADC is similar to triangle PDG and
thus, 
.
Now I will redraw segment FC while hiding segments
AD and BE.
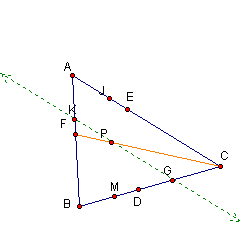
Using an argument similar to 1C. We can show that
triangle AFC is similar to triangle KFP and
thus, 
.
Since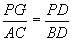 
and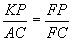 
,
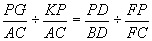
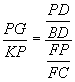
*Using substitution (1A),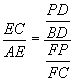 
.
PART 3
1A. Construct a line parallel to BC and passing through point P.
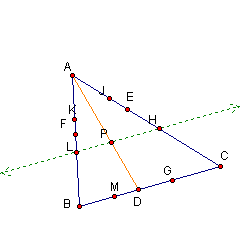
Using an argument
similar to 1A, we can show that triangle BAD is similar to triangle LAP.
Thus, 
.
Again using argument
1A we see that triangle DAC is similar to triangle PAH. Thus, 
.
By substitution,
.
By multiplying, we
see that 
.
1B. Now I will redraw
segment BE while hiding segments FC and AD.
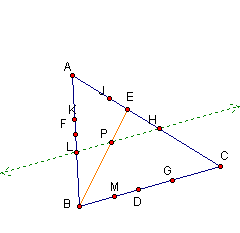
Using an argument similar to 1B. We can show that
triangle BEC is similar to triangle PEH and
thus, 
.
Now I will redraw segment FC while hiding segments
AD and BE.
Using an argument similar to 1C. We can show that
triangle FBC is similar to triangle FLP and
thus, 
.
Since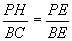 
and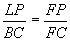 
,
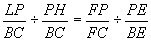
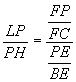
*Using substitution (1A),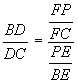 
.
Using the relationships
found in parts 1, 2 and 3 we see that
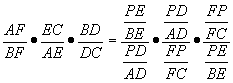
Therefore, we have
shown that given any triangle ABC with a point p in the interior and three
segments AD, FC and BE all passing through P, then 
.
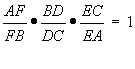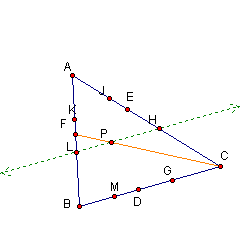
Can we generalize our findings to a point P outside of triangle ABC? Click Here and move point P outside triangle ABC. Can you still find the similar triangles?
Lets break it down into parts. First lets examine what happens when we construct a line JM parallel to side AB. First, we will look at it in relation to line PC.
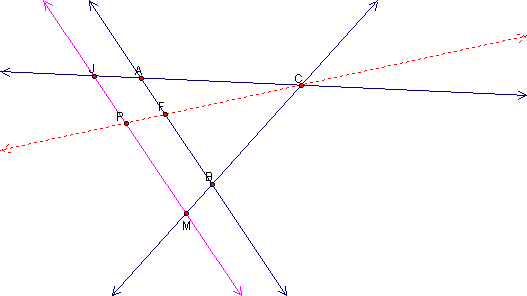
Even with P outside
of triangle ABC, we can see that similar triangles ACF and JCP are formed
as well as similar triangle FCB and PCM and can therefore use the same argument
(1A) we used when P was in the interior.
Click Here to investigate for yourself.
Move point P inside and outside of triangle ABC and see if you can find the
similar triangles.
Now lets look at line JM in relation to line BE.
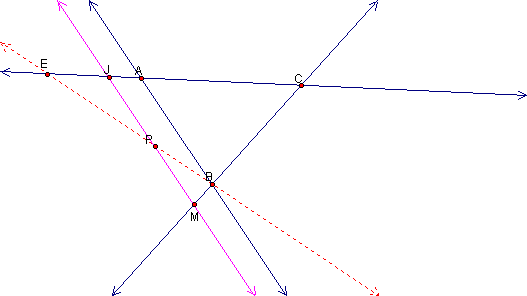
We can see that similar triangles AEB and JEP are formed even when P is outside of the triangle. Once again, we can use the same argument (1B) used previously to show that they are similar when point P was within the triangle.
Click Here to investigate for yourself. Move point P inside and outside of triangle ABC and see if you can find the similar triangles.
Now lets look at line JM in relation to line AD.
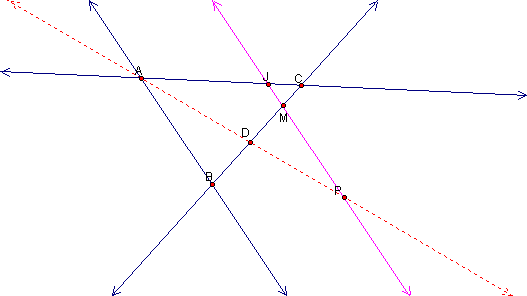
We can see that similar triangles ABD and PMD are formed even when P is outside of the triangle. Once again, we can use a similar argument (1C) to the one made when point P was within the triangle.
Click Here to investigate for yourself.
Move point P inside and outside of triangle ABC and see if you can find the
similar triangles.
In conclusion, it
appears that we have shown (and it can be proven) that given any triangle
ABC with a point P either in the interior or exterior and given the three
segments AD, FC and BE all passing through P, then 
.
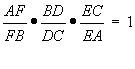Finally, using Geometers
Sketchpad we will show that the ratio of the areas of triangle ABC and triangle
DEF is always greater than or equal to 4.
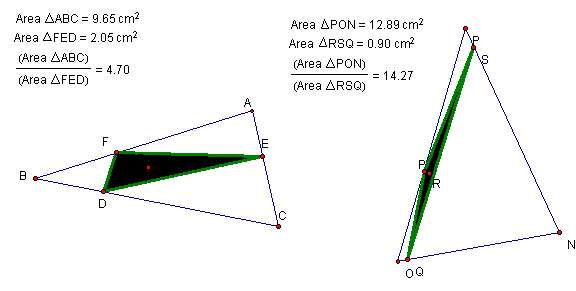
Click Here to try it for yourself.
When is the ratio
equal to 4?
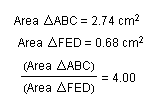
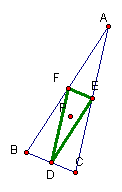
It is equal to four when points D, E, and F are the midpoints of the sides of triangle ABC.
Return to Janet Shiver's Home Page