Assignment
I
By: Sharren M. Thomas
The exploration is to examine graphs of
y = a sin (bx +
c) for different values of a, b, and
c.
Let's first begin by examine the graph when
a= 1; b = 1; and c = 0. Thus we have the sine graph with an amplitude of
1, x-intercepts occur
at πn where n is an integer, y-intercept of 0, and period of
2π.
![]()
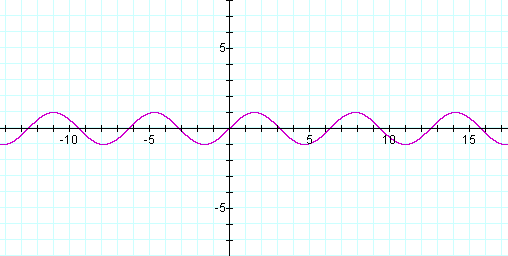
Now when a = 2; b = 1; and c = 0.
We have the graph of
![]()
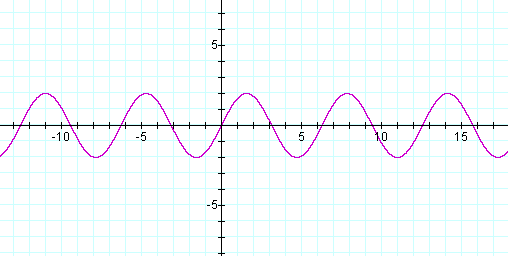
Notice that the graph y = sin x has been vertically stretched by a factor of 2. Each of the original y-coordinates of each point has been multiplied by 2. This is the largest y-coordinate of the graph, the amplitude of the graph. The period is still 2π.
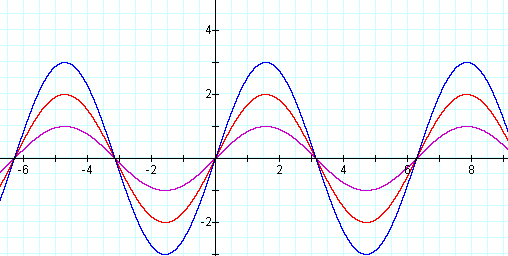
See below the graph of y = sin x for a = 1, 2, and 3. Notice that the graph of y = sin x is vertically stretched, but the period is not effected.
![]()
![]()
![]()
Click below to see what happens for different values of , a, the amplitude, when a is increased from 1 to 10, including all rational numbers in between Press play after you press below.
Let's examine what happens for a = -1.
Below examine the graph of
![]()
![]()
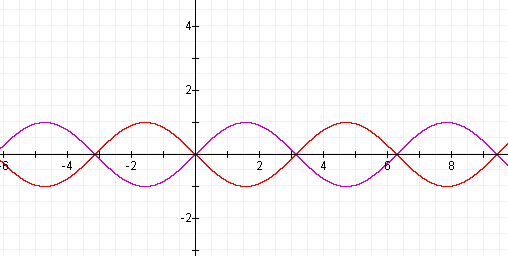
The graph y = sin x has been reflected
through the x- axis. Notice the amplitude for both graphs is still 1 and
the period is still 2π.
Click below to examine the graph y = a sin x
for negative values of a. Notice that the graph
y = sin x will be reflected through the
x - axis then vertically stretched as was for the positive values of a.
Click
Here Then
press play.
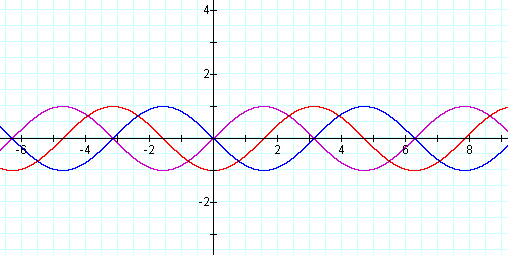
Now, let's examine the graph when a = 1; b
=1, 2, & 3; and c = 0. Thus we have the sine graph with amplitude of
1 but the graph
![]()
![]()
![]()
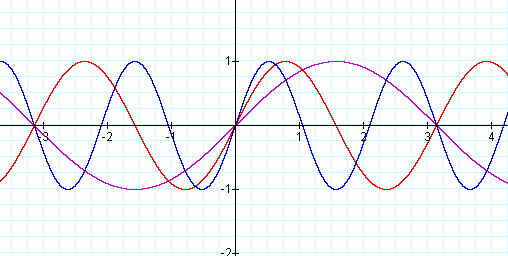
As you can see the original graph of y = sin x is being horizontally compressed by a factor of 1/b. Notice that this causes a change of the period. The period for the graphs
y = sin (bx + 0) is 2π / b.
Now, let's examine the graph when a = -1; b =-1, -2 & -3; and c = 0. Thus we have the sine graph with an amplitude of 1, but once again the period is changing or the graph y = sin (-x) is being horizontally compressed.
![]()
![]()
![]()
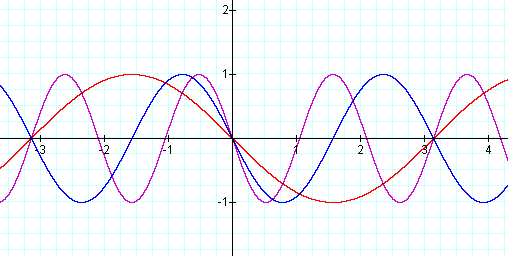
As you can see the original graph of y = sin x has been reflected across the x-axis and then the same as for the positive values of b, the graph is being compressed by a factor of 1/b.
Now, let's examine the graph y = a sin (bx+ c) when a = 1; b = 1; and c > 0.
![]()
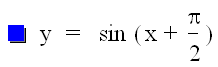
![]()
Notice that the graph has been shifted to the left. Each new graph has a phase shift -c/b.
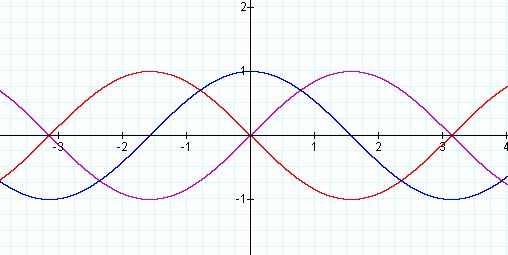
Now, let's examine the graph y = a sin (bx+ c) when a = 1; b = 1; and c < 0.
![]()
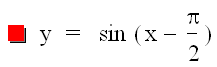
![]()