Quadratic Equations:
A Different Look
By: Kimberly Young
We often look at the graph of
quadratics. We are very interested in seeing how a,b, and c affect
the graph and the solutions. The solutions, or roots, are the
emphasis of this investigation.
Consider the equation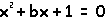 
. How do we
expect b to affect the roots of this equation? Let's consider
this graph on the xb-plane.
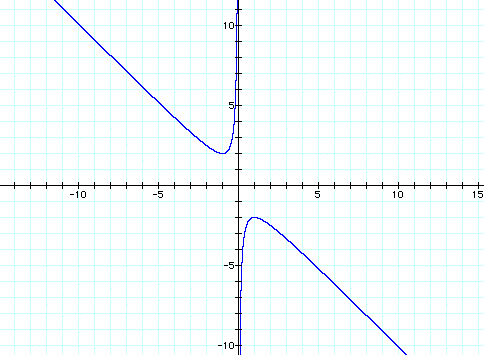
We can consider a specific b-value
and determine from the above graph if it will have a solution
and/or what the specific value(s) of the solution will be. Consider
b=4.
Notice that the line b=4 creates
a parallel line to the x-axis and the intersections point of the
line and the curve correspond to the solutions of the original
equation when b=4. Also, from looking at the graph on the xb-plane,
we see that the original equation has no solution when -2<b<2.
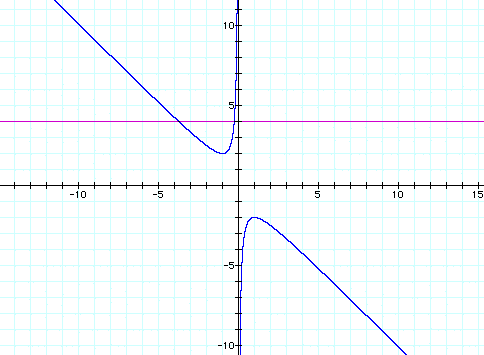
What happens to the graph
on the xb-plane as the value of c changes?
Consider the case when c=-1 rather
than +1. This yields the following graph. The blue graph is when
c=+1 and the red graph is when c=-1.
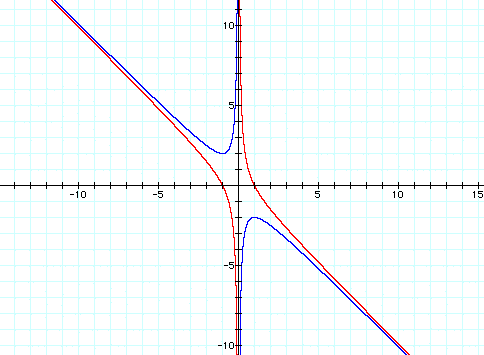
When c=-1, we can see that when
b is a particular value, the original equation will have two real
roots, one positive and one negative root.
This brings up the question,
for what values of c will I always have two solutions?
Consider the following animation.
The red line is a graph of the c-values when -10<c<10.
From this animation we can see
that different c-values affect the number of solutions for all
b. If c<0, there will always be two real roots, one positive
and one negative. When c=0, there will be only one real root.
When c>0, the original equation will either have two real roots,
one, or none.
We know from our studies of quadratic
equations the discriminante of the quadratic formula determines
the number of roots a quadratic equation has. Now the following
equation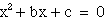 
corresponds following discriminant 
. When the discriminant
is negative, there are no real roots. So when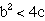 
there will be
no real solution. We can conclude:
-When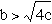 
, the equation
has two negative real roots.
-When
, the equation
has one negative real root.
-When 
, the equation
has no real roots.
-When 
, the equation
has one positive real root.
-When 
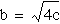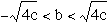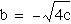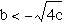, the equation
has two positive real roots.