Page Bird

Assignment 4
Centers of a Triangle

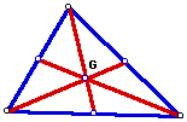
The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.

Click here to view a dynamic GSP centroid sketch. Just drag on a vertex to change the triangle.

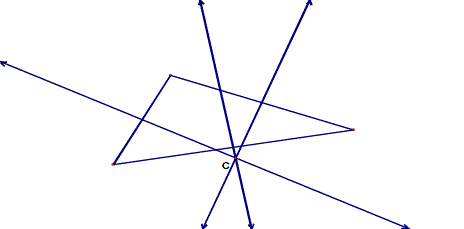
The orthocenter (H) of a triangle is the common intersection of the three lines containing the altitude. An altitude is a perpendicular segment from a vertex to the line
of the opposite side. The picture of the orthocenter (H) of triangle ABC is shown below.

Click here to see a dynamic GSP sketch of an orthocenter of a circle.

The circumcenter of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle.

The picture below shows the circumcenter of the triangle. Note that the circumcenter is not always inside the triangle, but often lies outside the triangle.

Another interesting point about the circumcenter is that it is the center of the circumscribed circle of the triangle.

Click here to see a GSP sketch of the circumcircle. To change the triangle, just drag on a vertex.

The incenter (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle.

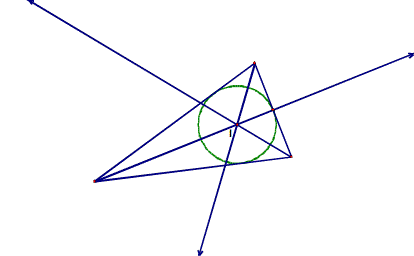
The picture below shows the incenter (I).

Note that the incenter is the center of the circle inscribed in the triangle. Click here to view a GSP sketch of the incenter. Just click on a vertex to change the shape of the triangle.

Now, if we look at the relationships among G, H, C, and I, we find that if the triangle is an isosceles triangle, then all the points lie on the same line or they are collinear. See the example below:

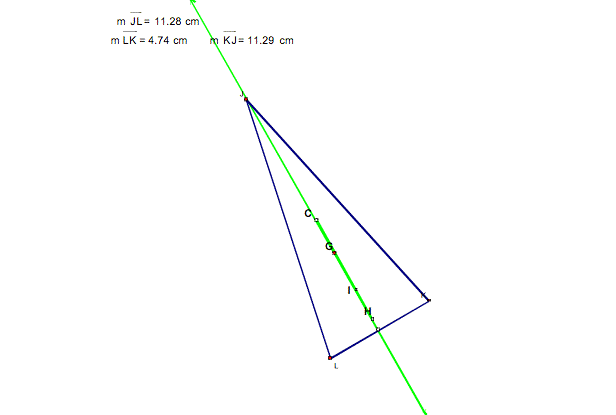
If the triangle is equilateral, then all the points are the same. That is to say, all the points are concurrent as seen in the picture below.

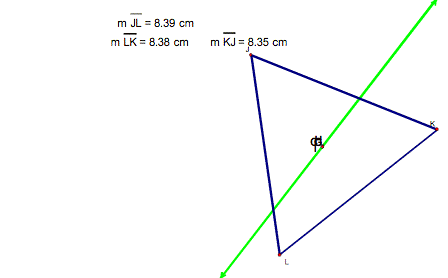
All the points except the incenter line on the same line regardless of the type of triangle. See the example below:

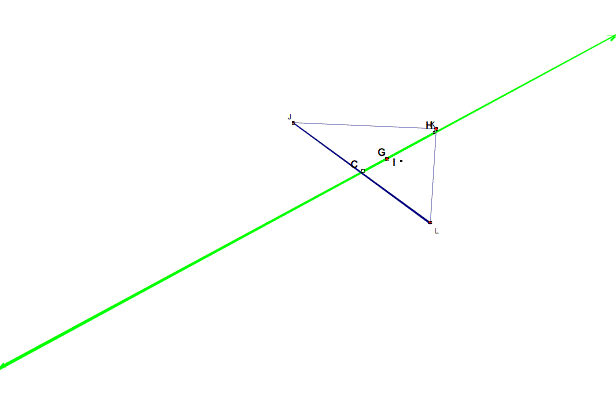
Click here to check out the different points on your own.

Return