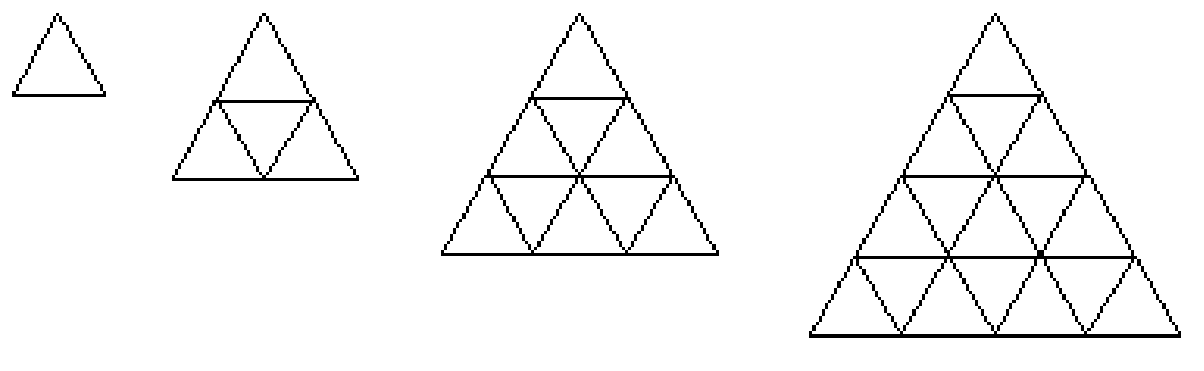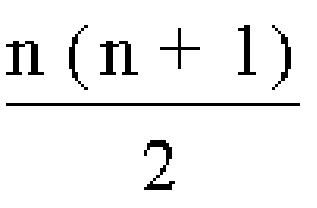Problem: Count the Triangles --
II
By Page Bird
Problem:
Count the triangles. Extend the sequence.
Hints/Solution:
Did you get 1, 5, 13, 27 so far?
How many triangles when there are five levels? 10 levels?
|
n
|
Triangluar Numbers |
Up |
Down |
Total Trianlges |
| 1 |
1 |
1 |
0 |
1 |
| 2 |
3 |
4 |
1 |
5 |
| 3 |
6 |
10 |
3 |
13 |
| 4 |
10 |
20 |
7 |
27 |
| 5 |
15 |
35 |
13 |
48 |
| 6 |
21 |
56 |
22 |
78 |
| 7 |
28 |
84 |
34 |
118 |
| 8 |
36 |
120 |
50 |
170 |
| 9 |
45 |
165 |
70 |
235 |
| 10 |
55 |
220 |
95 |
315 |
How do you verify your sequence?
I was able to come up with the above table after making a sketch
pad drawing such as the one below and then making a table on my
notebook paper. I took the hint about number of triangles that
point up and down and was able to see a pattern.
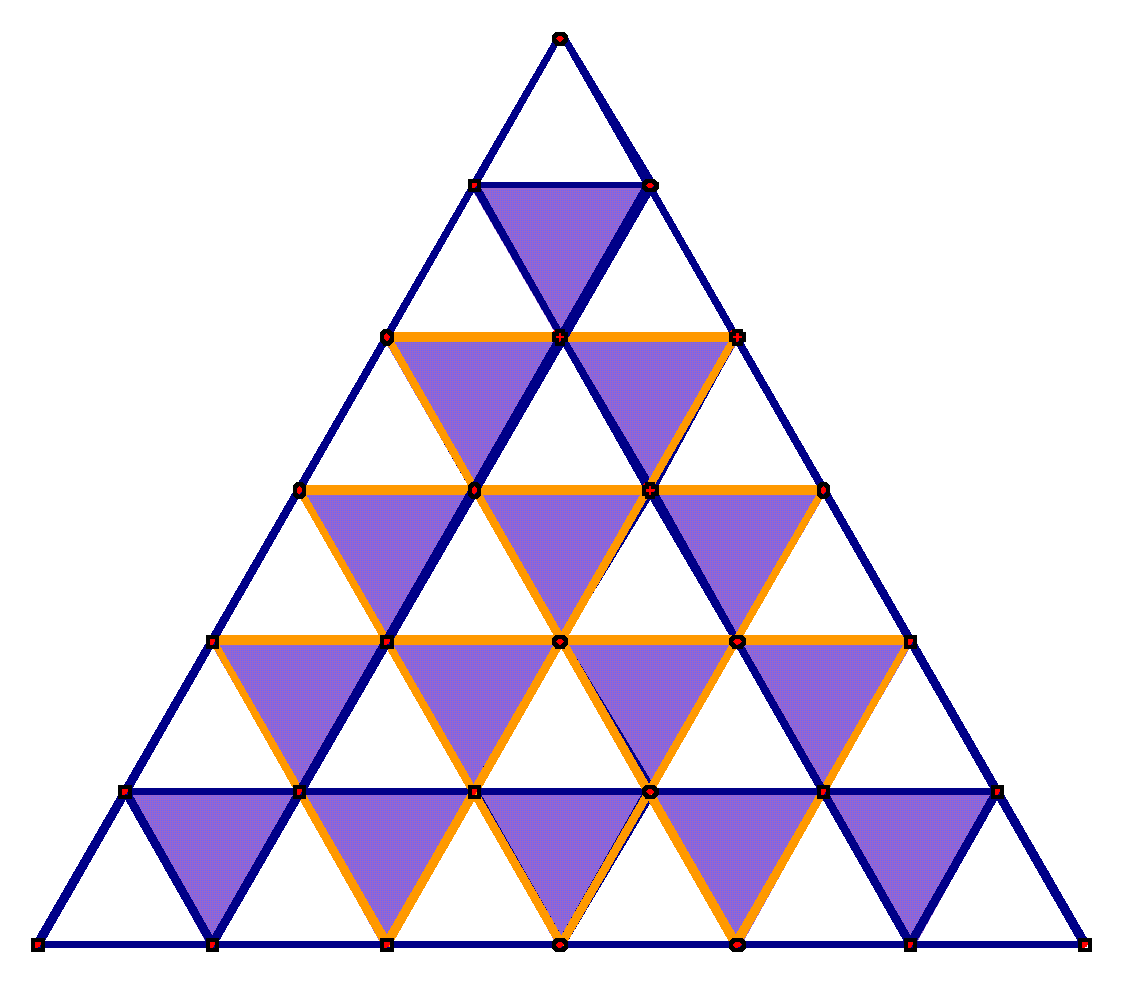I was able to make the table above
to n=6 based strictly on my drawings.
My next question was could I come up with a general
formula for n levels?
There is probably a more concise
way to write this, however this worked for my excel explorations:
Let t(n)= the number of triangles for a given n level
Then t(n) = the number of triangles
that point up plus the number of triangles that point down.
The number that point up can be
found by
the summation of T(n), where T(n) is
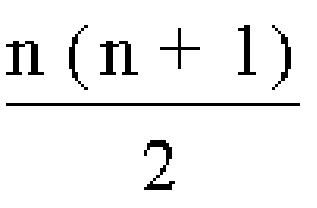
and n begins at 1 and continues until the nth level.
The number of triangles that point down can be found by
dn=
T(n -1)-dn-1
Where d is the number of triangles pointing down.
Therefore the total number of triangles can be found by
Total = T(n-1)- dn-1 + S T(n)
Click here to
return to my Emat 6690 page