

Here we will investigate the graphs involving
![]() and
and ![]() . We will start
with
. We will start
with ![]() .
.
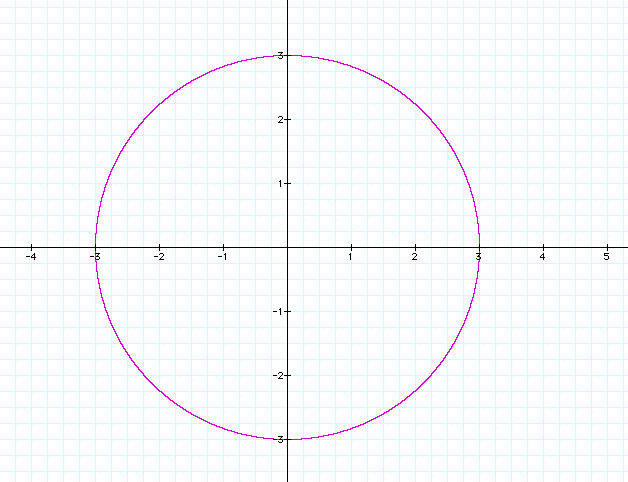
This is probably no surprise if you remember
that an equation of the form ![]() defines
a circle with center at the origin and radius = r.
defines
a circle with center at the origin and radius = r.
Now, add xy to the expression, so we have ![]() .
.
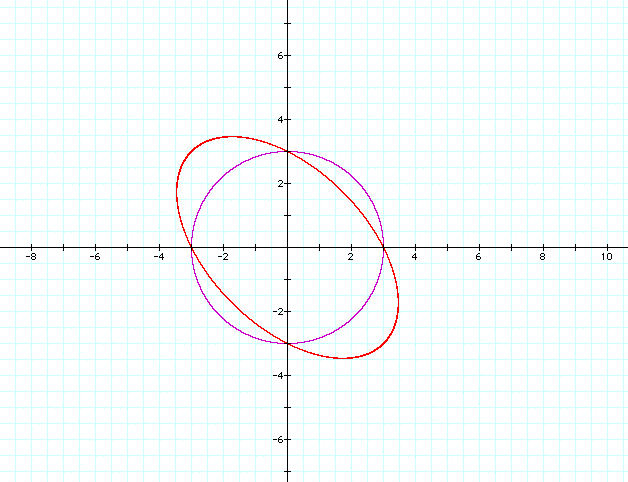
Now lets vary the coefficient of the xy term,
we'll call it a, ![]()
 a=.5
a=.5
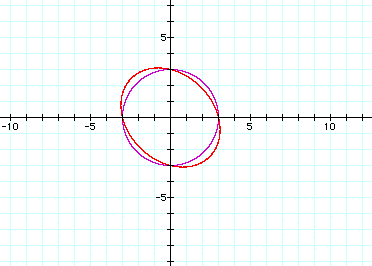
 a=1
a=1
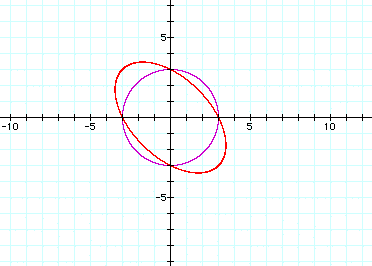
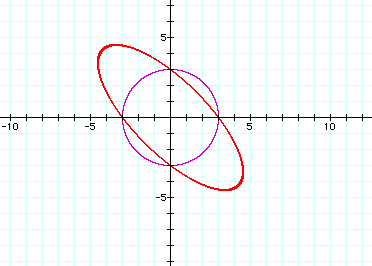 a=1.5
a=1.5
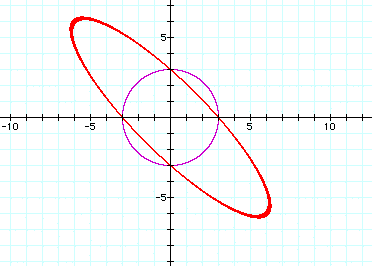 a=1.75
a=1.75
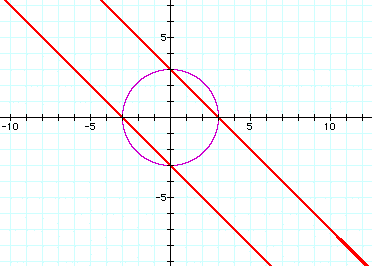 a=2
a=2
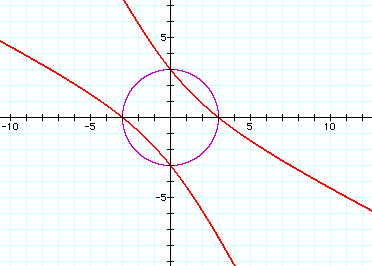 a=2.5
a=2.5
Note that it appears that as a increases from 0 (the circle equation) to a=2, it first appears to be an ellipse then "opens up" to look like two lines around a=2. For a>2, it appears to be two hyperboli.
Now lets look at a<0.
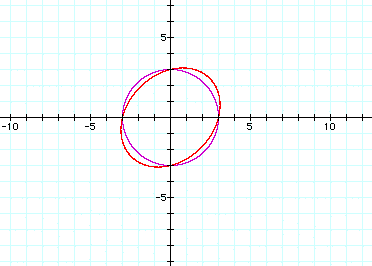 a=-.5
a=-.5
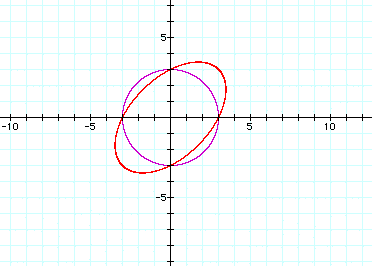 a=-1
a=-1
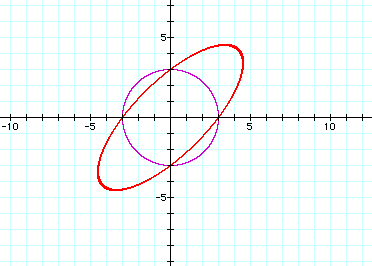 a=-1.5
a=-1.5
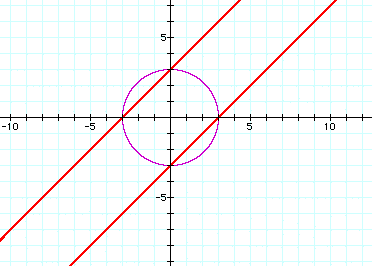 a=-2
a=-2
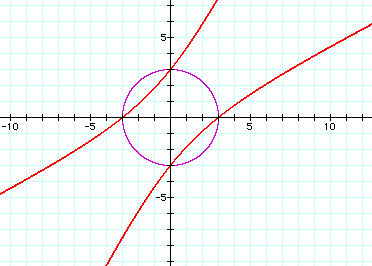 a=-2.5
a=-2.5
For a<0, we see a similar pattern. The circle opens up to look like an ellipse, then two parallel lines at a=-2, then two hyperboli.
Click here to see an animation of this as a varies between -4 and 4.