A parametric curve in the plane is a pair of functions

x = f(t)

y = g(t)

where the two continuous functions define ordered pairs (x,y).

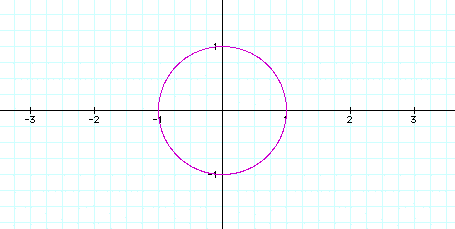
Graph

x=cos(t)

y=sin(t)

for 0<t<2pi

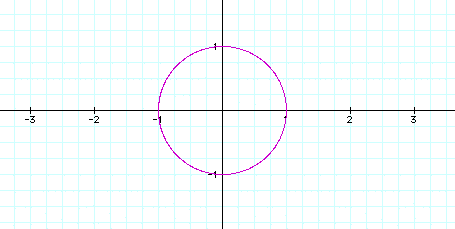
Graph

x=cos(at)

y=sin(bt)

where a=1, b=1 and 0<t<2pi

Let's see what happens when we change the values of a and b. What happens when a=1, but b=2?

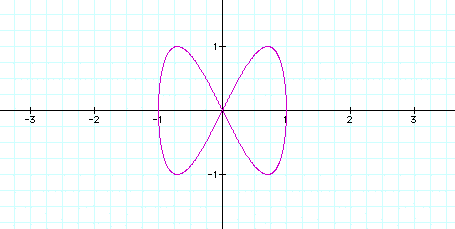
Notice that it divided the shape into two parts. What about when a=1 and b=3?

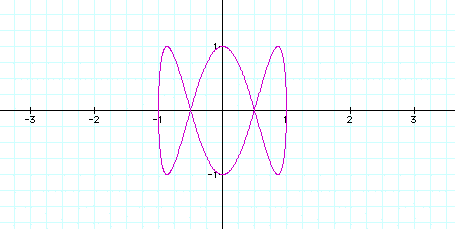
Notice that the new value for b divided the graph into three parts. Can you guess what might happen when we change the value of b to 4?

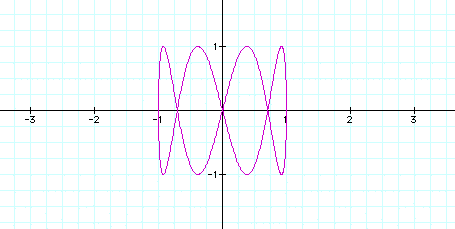
That's right. It divided the shape into four parts. Now let's see what happens when we change the value of a. Here is what happens when a=2 and b=1.

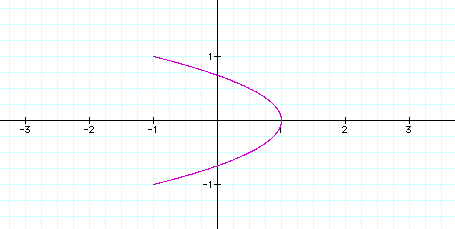
Before we make any assumptions let's try another value for a. Here is what happens when a=3 and b=1.

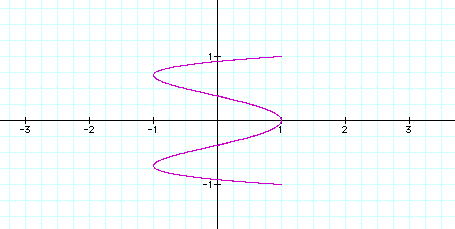
Notice for a=2 we got an open graph, but for a=3 we got a closed graph. What do you think will happen for a=4? a=5?

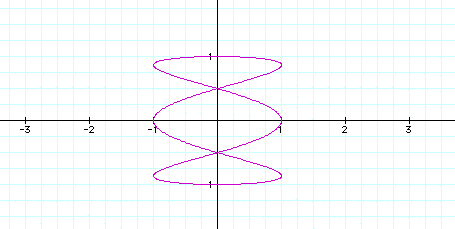
a=4, b=1

a=5, b=1

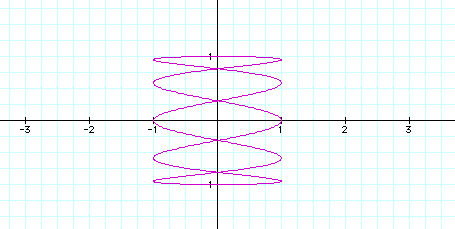
What do you think will happen when we change the values of a and b at the same time?

a=2, b=3

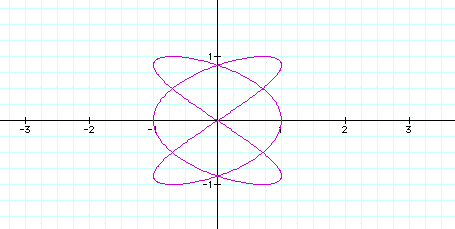
 Return to Home Page