Investigation
If we set
for b = -3,-2,-1,0,1,2,3, and overlay the graphs, the following picture is obtained.
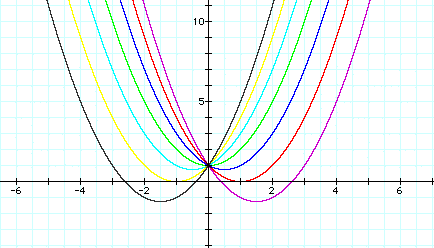
Now we can find the locus of each parabla.
(1.5,
-1.25)
(1,
0)
(.5,
.75)
(0,
1)
(-.5,
.75)
(-1,
0)
(-1.5,
-1.25)
Now let's plot the locus point only of each parabola.
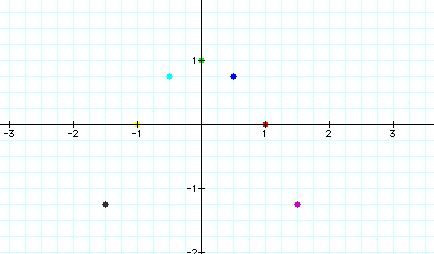
Notice that the points form what looks like a concave down parabola with the locus at (0,1). We can see from the picture that the roots of the new parabola are x=-1 and x=1. Let's try to find the equation of the new parabola.
First set y equal to the roots.
y=(x+1)(x-1)
y=x^2 -1
But because this is a concave down parabola the x^2 must be negative, so let's see what happens when we graph y=-x^2+1.
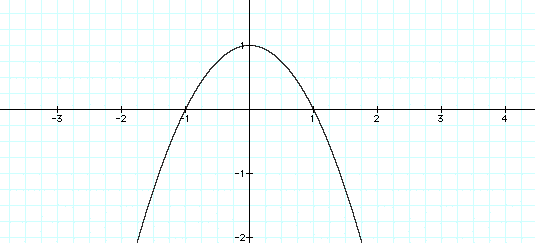
Here is what we get when everything is graphed together.
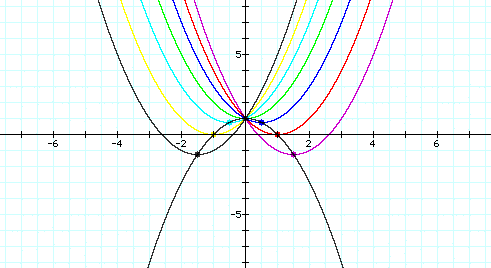
Return to Homepage