Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find.

First, let us define a medial triangle. The triangle formed by the line segments joining the three medians of a triangle is called the medial triangle.

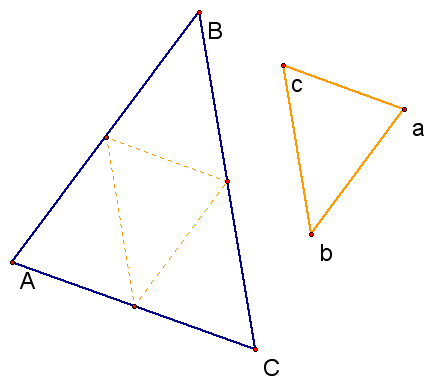
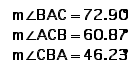
 We can see from the information given above that the orginal triangle and the medial triangle are similar. If two angles of one triangle are equal to two angles of another triangle, then the triangles are similar, but are the triangles congruent? Let's do some investigating.

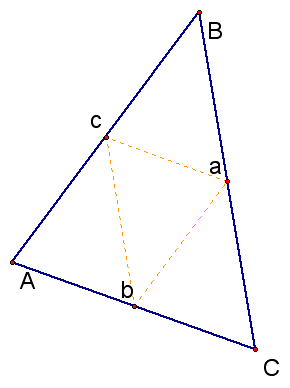
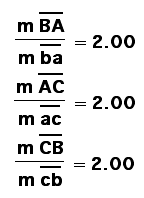
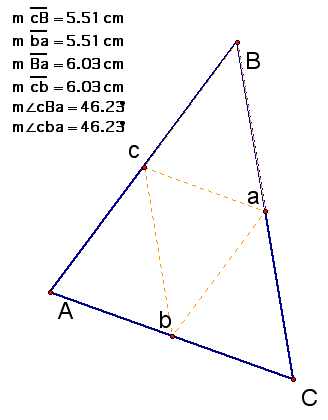
ca appears to be ll to AC

Here is our proof:

(I have changed some of the letters so that we get a better understanding)

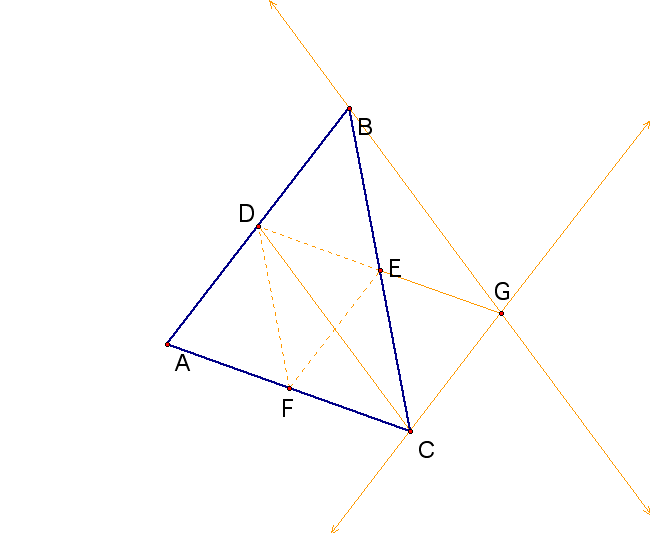
Given:

D is the midpoint of AB

E is the midpoint of BC

Now we construct lines BG ll to DC and CG ll to DB.

Angle DEB is congruent to angle CEG by vertical angle theorem.

Angle CBA is congruent to angle BCG by alternating interior angles theorem.

Therefore, triangle DEB is congruent to triangle CEG by ASA.

Then segement DB is congruent to segment AD is congruent to segment CG by congruent triangles.

Angle ADC is congruent to angle GCD by alternating interior angles theorem, and triangle ADC is congruent to triangle GCD by SAS.

Since we know that DG is congruent to AC by congruent triangles, then segment DE is 1/2 AC, since DE is 1/2 DG.

It follows ADGC is a parallelogram, and DE ll AC.

Now back to our original triangle:

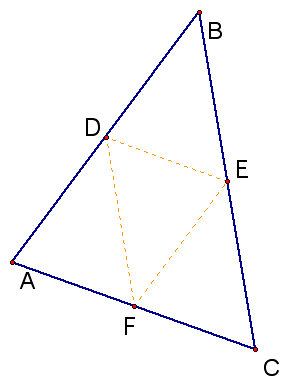
Since we have proven that segment DE ll segement AC, then this will hold true for each median. Hence, FE ll AB and FD ll CB. Wd can now show that all four triangles are congruent by SAS or SSS, and the medial triangle is similar to the original.

Return to Home Page