What is a Pedal Triangle?

Let triangle ABC be any triangle. If P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC is the pedal triangle for the point P. XYZ forms the pedal triangle.

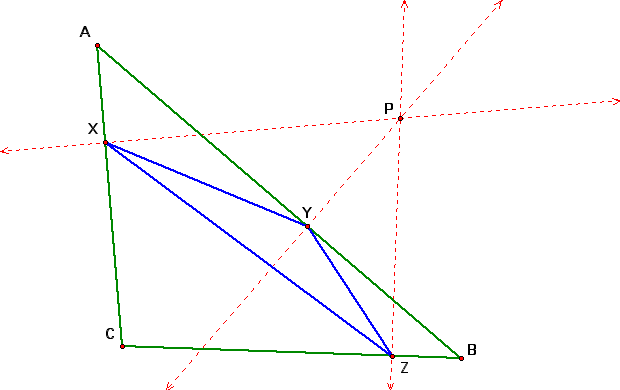
Let's do some investigating.

1. What if the pedal point P is the Centroid of triangle ABC? First construct the Centroid point G.

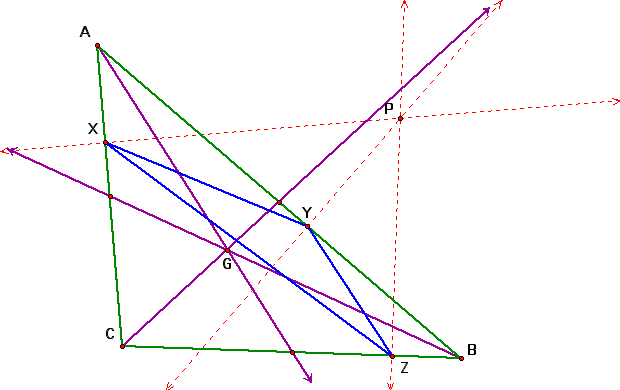
Notice the when point P is moved to point G the pedal triangle changes shape.

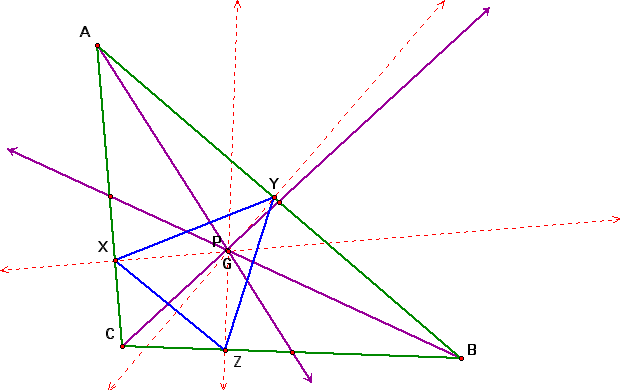
2. What if the pedal point P is the Incenter of triangle ABC? First, construct the Incenter point I.

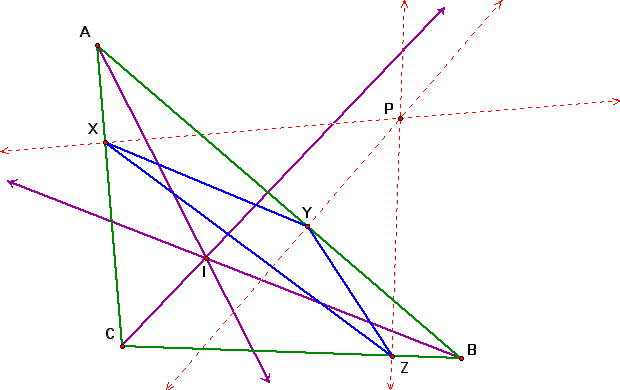
Notice what happens when point P is moved to point I.

3. What if the pedal point P is the Orthocenter of triangle ABC? We will first construct the Orthocenter(H) of ABC. Notice that the Orthocenter is outside ABC.

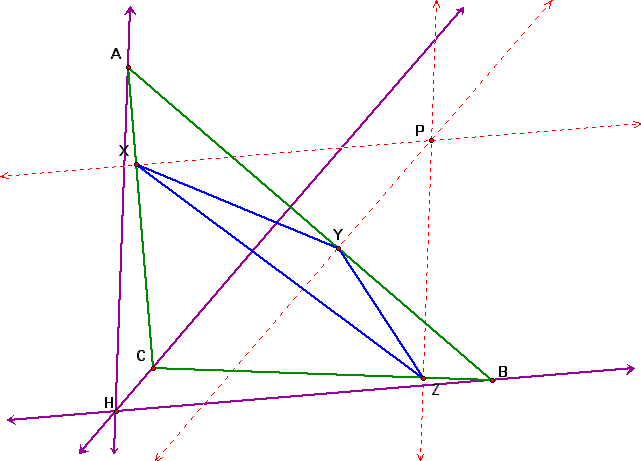
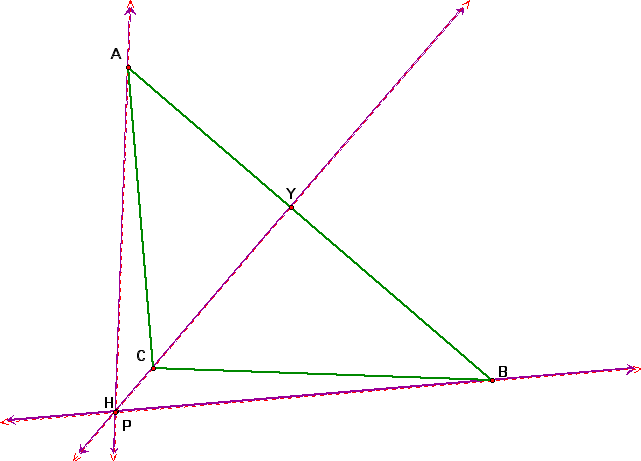
4. Let's adjust our original triangle ABC so that the Orthocenter is inside the triangle. Notice what happens to the pedal triangle.

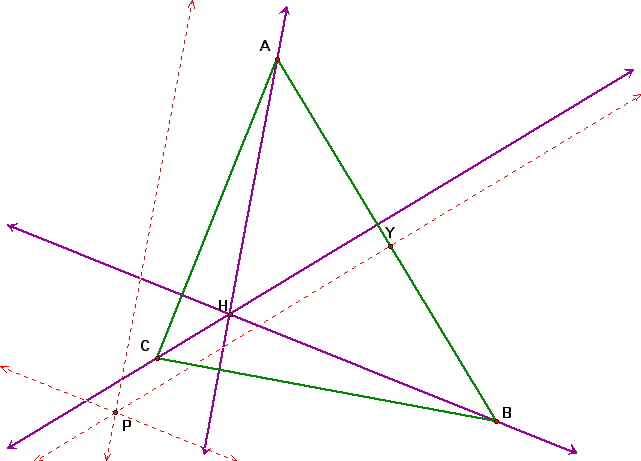
What if pedal point P is the Circumcenter of triangle ABC?

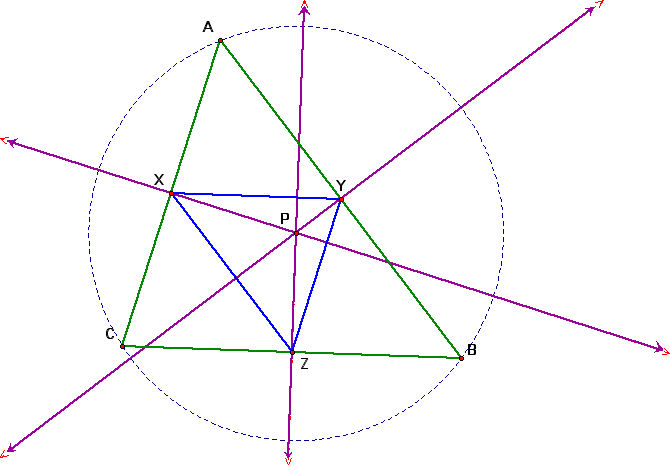
What if the Circumcenter is located outside of triangle ABC?

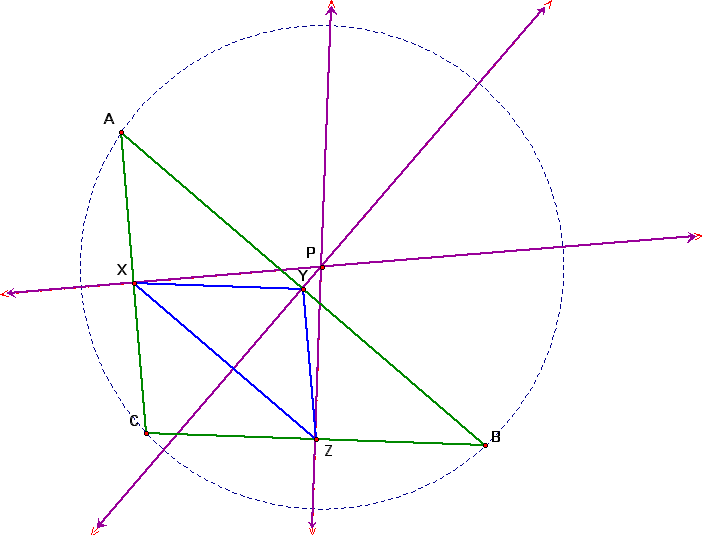
What if P is on a side of triangle ABC?

We can see what happens when P is on the side of ABC. In this example Y and P become the same point. This would be true for any side of ABC.

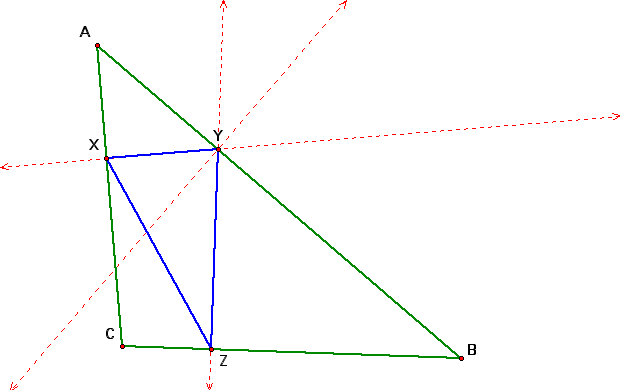
What if P is one of the vertices of triangle ABC?

Return to Home Page