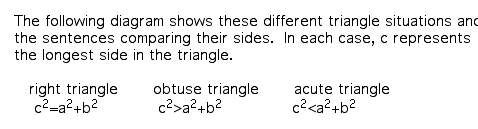
Definition:

Theorem:(Converse of the Pythagorean Theorem) - If a triangle has sides of lengths a, b and c where c is the longest length and c^2 = a^2 + b^2, then the triangle is a right triangle with c its hypotenuse.

Variations of the Converse of the Pythagorean Theorem can be used to classify a triangle as right, obtuse, or acute.

Theorem: If a, b, and c represent the lengths of the sides of a triangle, and c is the longest length, then the triangle is obtuse if c^2 > a^2 + b^2, and the triangle is acute if c^2 < a^2 + b^2.

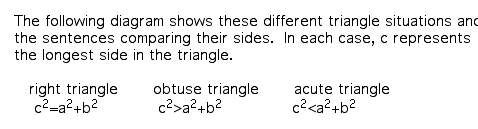
Sample Problems:

Example 1:

Proof: Prove that a, b, and c are a Pythagorean triple, then ka, kb, and kc (where k > 0) represent the side lengths of a right triangle.

Example 2:

Return to Instructional Unit