

A spreadsheet can be used to estimate growth of a savings account after 30 years when the initial deposit is $1000 and it grows at 5.9% interest compounded monthly.
| Year | Account Balance |
| 1 | 1060.62 |
| 2 | 1124.92 |
| 3 | 1193.11 |
| 4 | 1265.44 |
| 5 | 1342.15 |
| 6 | 1423.52 |
| 7 | 1509.82 |
| 8 | 1601.34 |
| 9 | 1698.42 |
| 10 | 1801.38 |
| 11 | 1910.58 |
| 12 | 2026.41 |
| 13 | 2149.25 |
| 14 | 2279.54 |
| 15 | 2417.73 |
| 16 | 2564.30 |
| 17 | 2719.76 |
| 18 | 2884.63 |
| 19 | 3059.50 |
| 20 | 3244.98 |
| 21 | 3441.69 |
| 22 | 3650.34 |
| 23 | 3871.62 |
| 24 | 4106.33 |
| 25 | 4355.27 |
| 26 | 4619.29 |
| 27 | 4899.32 |
| 28 | 5196.33 |
| 29 | 5511.34 |
| 30 | 5845.45 |
The following compound interest formula was used to determine the amounts at the end of each year:
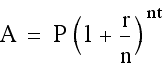
The spreadsheet was able to calculate the amounts, A, given the values P = 1000, r = .059, n = 12, and t was assigned the values in the year column.
Suppose interest was compounded yearly at 12.5% using the same principal amount (r = .125, n = 1):
| Year | Account Balance |
| 1 | 1125.00 |
| 2 | 1265.62 |
| 3 | 1423.83 |
| 4 | 1601.81 |
| 5 | 1802.03 |
| 6 | 2027.29 |
| 7 | 2280.70 |
| 8 | 2565.78 |
| 9 | 2886.51 |
| 10 | 3247.32 |
| 11 | 3653.24 |
| 12 | 4109.89 |
| 13 | 4623.63 |
| 14 | 5201.58 |
| 15 | 5851.78 |
| 16 | 6583.25 |
| 17 | 7406.16 |
| 18 | 8331.92 |
| 19 | 9373.42 |
| 20 | 10545.09 |
| 21 | 11863.23 |
| 22 | 13346.13 |
| 23 | 15014.40 |
| 24 | 16891.20 |
| 25 | 19002.60 |
| 26 | 21377.93 |
| 27 | 24050.17 |
| 28 | 27056.44 |
| 29 | 30438.49 |
| 30 | 34243.30 |
Suppose in the original problem, the interest was compounded daily (n = 365):
| Year | Account Balance |
| 1 | 1060.77 |
| 2 | 1125.23 |
| 3 | 1193.61 |
| 4 | 1266.15 |
| 5 | 1343.09 |
| 6 | 1424.71 |
| 7 | 1511.29 |
| 8 | 1603.14 |
| 9 | 1700.56 |
| 10 | 1803.90 |
| 11 | 1913.52 |
| 12 | 2029.81 |
| 13 | 2153.16 |
| 14 | 2284.01 |
| 15 | 2422.81 |
| 16 | 2570.04 |
| 17 | 2726.23 |
| 18 | 2891.90 |
| 19 | 3067.64 |
| 20 | 3254.06 |
| 21 | 3451.81 |
| 22 | 3661.58 |
| 23 | 3884.10 |
| 24 | 4120.13 |
| 25 | 4370.51 |
| 26 | 4636.11 |
| 27 | 4917.85 |
| 28 | 5216.71 |
| 29 | 5533.73 |
| 30 | 5870.01 |