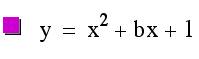
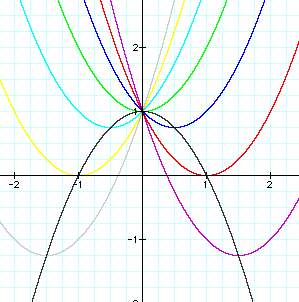
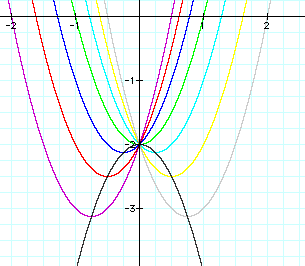
Lets begin by taking a look at graphs when b={-3,-2,-1,0,1,2,3}.
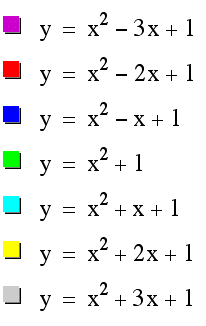
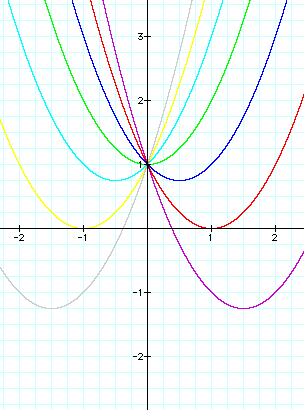
These graphs appear to produce parabolas which overlap each other and form a nice pattern. For instance if we look at the graphs of those equations produced by b and -b they appear to reflect around the x axis, that is to be symmetric with respect to it.
If we focus in on the vertices of these parabolas
we notice that plotting the vertices only that indeed these vertex
points seem to describe a parabolic equation. This parabola has
vertex point at (0,2) and opens down. From previous discussions
about parabolas we conjecture that the parabola that passes through
the vertex points of the parabolas above is described by the equation
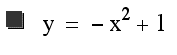. Graphing this
equation confirms this conjecture.
Observing the relationship between the parabola
that passes throught the vertex points and the family of parabolas
that produce those vertex points we are ready to establish another
conjecture. For the graphs of parabolas formed by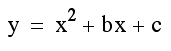 
where
c is any constant value and b varies, the equation which graphs
as a parabola that passes through the vertices of these parabolas
is 
. Lets try another example to test
our conjecture.
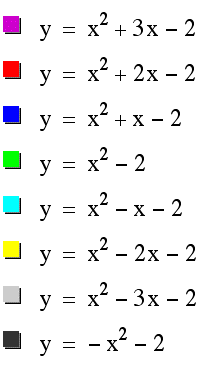
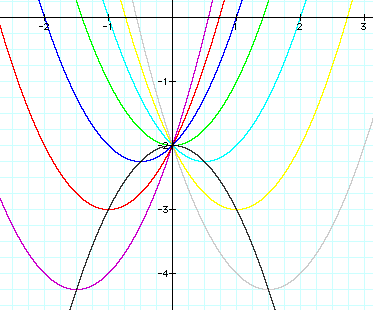
This result seems to confirm our conjecture. We will look later at trying to prove that these parabolas always intersect at the vertex points.
What happens to our hypothesis as a varies from 1? Lets look at an example of this.
So to take our conjecture one step further,
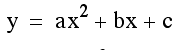describes a set of parabolas as
a and c are some fixed values and b varies. The equation of the
parabola which will pass through the vertex points of all such
parabolas is 
. how may we begin to prove such
a conjecture?
Lets begin by looking at an concrete example
of what we are trying to show. Using our last example above lets
find the points of intersection between 
and
. This equates to
solving the following equation;
= 
x(4x+1)=0
x=0 0r x=-1/4. Therefore, substituting for x and solving for y, the points of intersection are (0,-2) and (-1/4,-17/8). Is (-1/4,-17/8) the vertex of the parabola? Lets find it by algebraic methods.
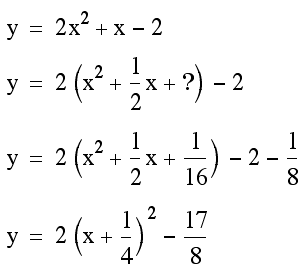
The vertex of the parabola is indeed (-1/4,-17/8). the general case and the proof are much similar to the specific case. Lets first find the vertex point for the parabola
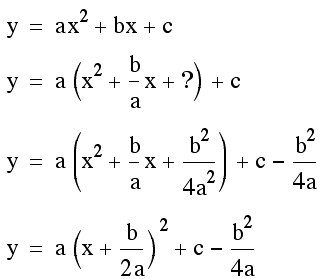
So the vertex point is defined (-b/2a,c-bsquared/4a) Will this always be the point of intersection?
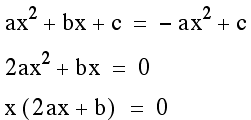
So x=0 or (2ax+b)=0. If 2ax+b=0, then 2ax=-b. Therefore x=-b/2a. Substituting we get
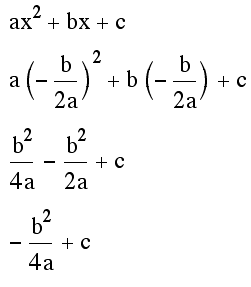for y.